Dans cette section

Rappel

$c^2 = a^2 + b^2$

$a^2 = c^2 – b^2$

$b^2 = c^2 – a^2$

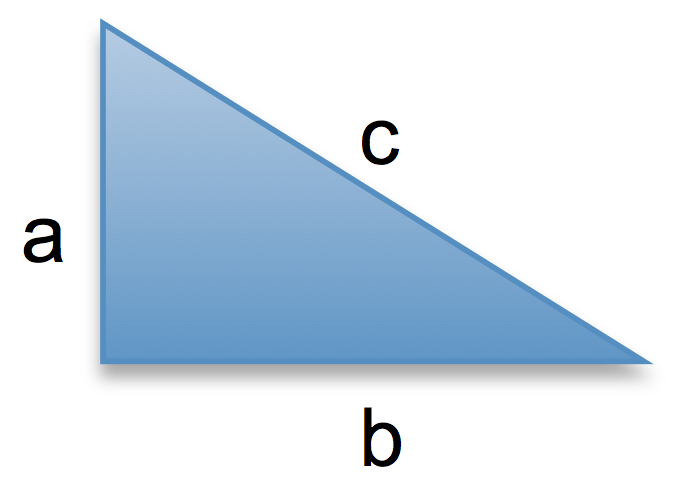
Schéma d’un triangle rectangle de côtés a et b et d’hypoténuse c

Trucs et astuces

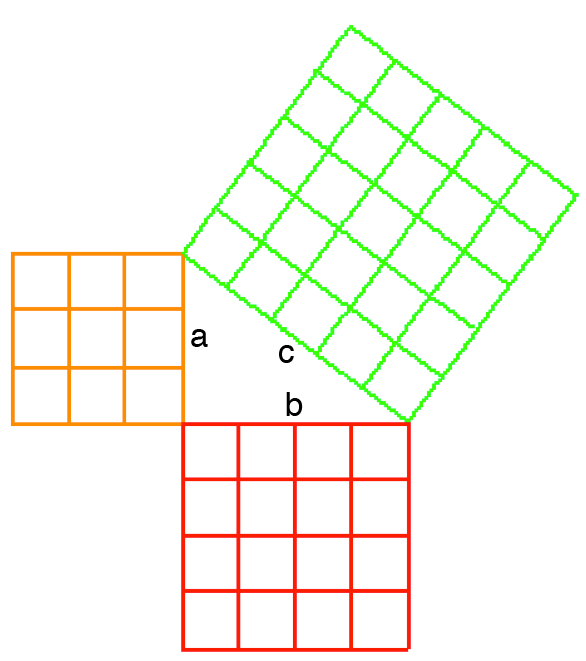
La méthode 3-4-5 est souvent utilisée comme référence par les travailleurs des métiers de la construction. Il s’agit en fait du théorème de Pythagore. Pour démontrer ce théorème, on utilise un triangle droit avec des côtés mesurant 3 pouces, 4 pouces et 5 pouces (ou 3, 4 et 5 pieds ou verges ou toute autre unité).

Si vous multipliez la longueur de chaque petit côté par elle-même et que vous additionnez ces deux résultats, vous obtenez un total représentant la longueur du dernier côté multiplié par lui-même :

$(3 \times 3) + (4 \times 4) = (5 \times 5)\ \text{ou}\ 3^2 \times 4^2 = 5^2$
donc $a^2 + b^2 = c^2$ et $c = \sqrt{a^2 + b^2}$

Schéma d’un triangle rectangle de côtés a et b et d’hypoténuse c, formé par un carré orange de 3 unités pour le côté a, un carré rouge de 4 unités pour le côté b et un carré vert de 5 unités pour le côté c.

Résolution de problème

  1. Dessiner un croquis en indiquant les mesures données
  2. Choisissez la formule à utiliser
  3. Calculez la réponse

Pour vérifier l’équerrage d’un terrain, on utilise le calcul trigonométrique de la diagonale :

Donc : $\sqrt{98\text{,}167^2 + 40\text{,}5^2} = 106\text{,}193'$

Soit : $106'\text{-}2 \frac{5}{16}''$

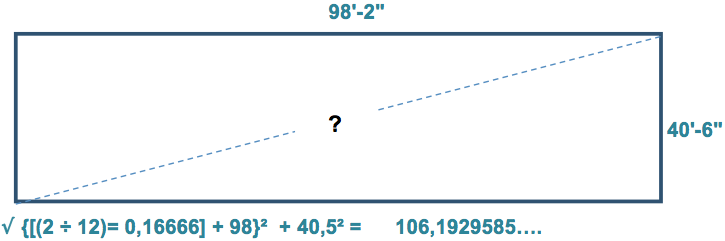
Schéma d’un terrain de 98'-2'' de long par 40'-6'' de large. Quelle est la diagonale du terrain ?

Sur la calculatrice, indiquez :

  1. $98\text{,}167$
  2. x2
  3. +
  4. $40\text{,}5$
  5. x2
  • $= 11277\text{,}00989$
  1. √

$106\text{,}1929585$... = $106'-$ ?"

Trucs et astuces

On multiplie les décimales par 12 pour obtenir le nombre de pouces.
$106\text{,}1929585...\ – 106 = 0\text{,}1929585... \times 12 = 2\text{,}315502534... = 2''$

Soit : $106' - 2\frac{\text{? }}{\text{? }}''$

Trucs et astuces

On multiplie les décimales par 16 pour obtenir la fraction du pouce. $2\text{,}315502534...\ – 2 = 0\text{,}315502534... \times 16 = 5\text{,}048040552...\ = \frac{5}{16}$

Soit : $106'\text{-}2 \frac{5}{16}''$

À vous

1. La diagonale du terrain : Calculez la diagonale du terrain en système métrique.

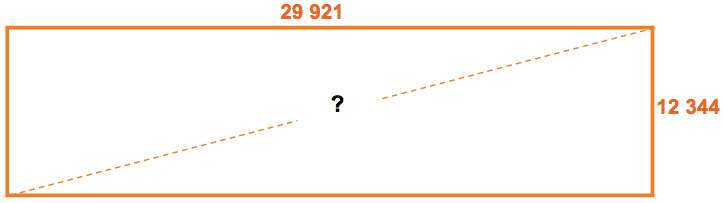
Schéma d’un terrain de 29 921 mm de long par 12 344 mm de large. Quelle est la diagonale du terrain ?

mm

32367 globals.frenchFormatNumber(ANS_R)

Donc : $\sqrt{29\,921^2 + 12\,3442} = 32\,367\ \text{mm}$

Sur la calculatrice, indiquez :

  1. $29\text{,}921$
  2. x2
  3. +
  4. $12\text{,}344$
  5. x2
  • $= 1047\text{,}640$
  1. √
  • $= 32\text{,}367$

Aucune transformation n’est requise autre que retirer la virgule et laisser un espace entre les mètres et les millimètres.

La bonne réponse est : ANS mm

À vous

2. Le limon d’un escalier

Les charpentiers effectuent des calculs qui les aident à dessiner et à construire un escalier en bois. Calculez la longueur du limon (c) pour l’escalier illustré ci-dessous :

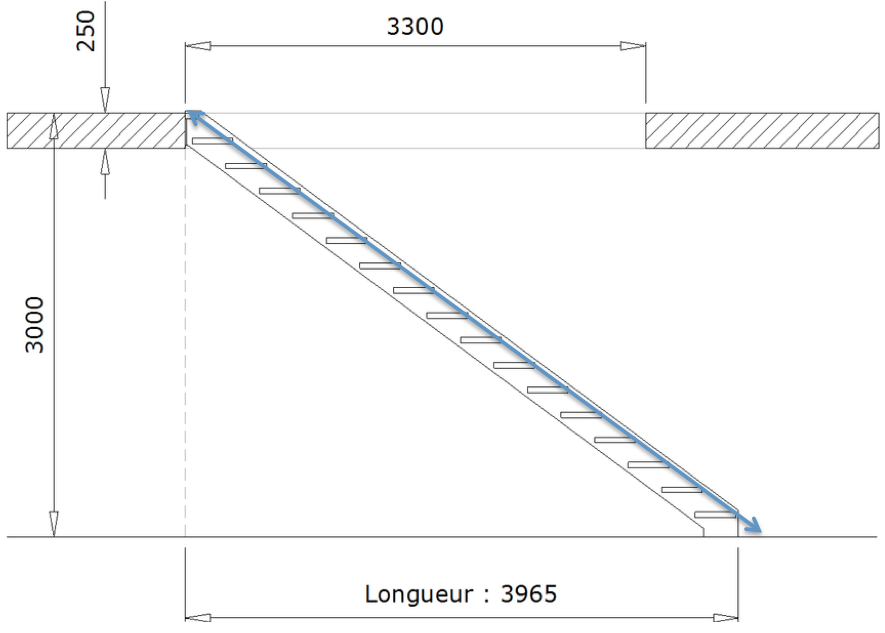
Schéma du limon d’un escalier avec mesures en millimètres.

Distance totale de la montée (a) : $3\,000$ mm

Distance totale de l’étendue (b) : $3\,965$ mm

Longueur du limon (c) : $c^2 = a^2 + b^2$

mm

4972 globals.frenchFormatNumber(ANS_R)

La bonne réponse est : ANS mm

$\sqrt{3000^2 + 3965^2} = 4\,972\ \text{mm}$