Rappel
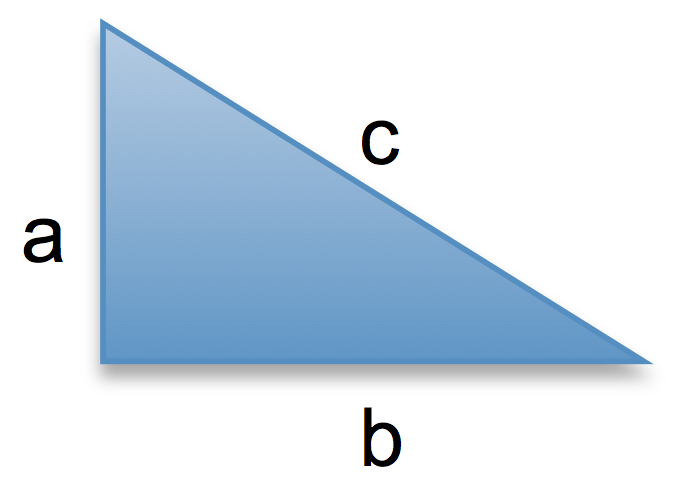
$c^2 = a^2 + b^2$
$a^2 = c^2 – b^2$
$b^2 = c^2 – a^2$
Trucs et astuces
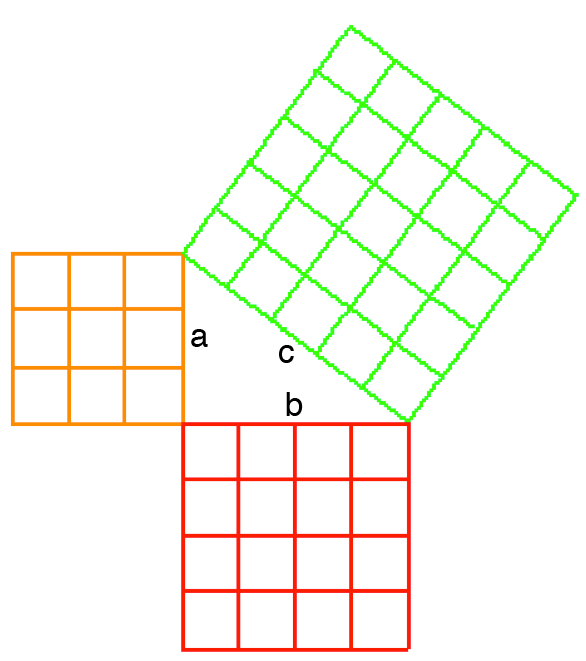
La méthode 3-4-5 est souvent utilisée comme référence par les travailleurs des métiers de la construction. Il s’agit en fait du théorème de Pythagore. Pour démontrer ce théorème, on utilise un triangle droit avec des côtés mesurant 3 pouces, 4 pouces et 5 pouces (ou 3, 4 et 5 pieds ou verges ou toute autre unité).
Si vous multipliez la longueur de chaque petit côté par elle-même et que vous additionnez ces deux résultats, vous obtenez un total représentant la longueur du dernier côté multiplié par lui-même :
$(3 \times 3) + (4 \times 4) = (5 \times 5)\ \text{ou}\ 3^2 \times 4^2 = 5^2$
Donc
| $c^2 = a^2 + b^2$ | $c = \sqrt{a^2 + b^2}$ |
| $a^2 = c^2 - b^2$ | $a = \sqrt{c^2- b^2}$ |
| $b^2 = c^2 - a^2$ | $b = \sqrt{c^2- a^2}$ |
Résolution de problème
- Dessiner un croquis en indiquant les mesures données
- Choisissez la formule à utiliser
- Calculez la réponse
Pour vérifier l’équerrage d’un terrain, on utilise le calcul trigonométrique de la diagonale :
Donc : $\sqrt{5\text{,}25^2 + 5\text{,}25^2} ≈ 6\text{,}175''$

Sur la calculatrice, indiquez :
- 5,25
- 3,25
- = 38,125
- = 6,174 544 517 61
À vous
Échelle
L'échelle de 24 pieds ci-contre est utilisée pour établir une connexion d’entrée de service sur un bâtiment. Le bas de l'échelle ne peut pas être à plus de six pieds de l’immeuble. Quelle est la hauteur minimale à laquelle l’échelle sera en contact avec le bâtiment ?
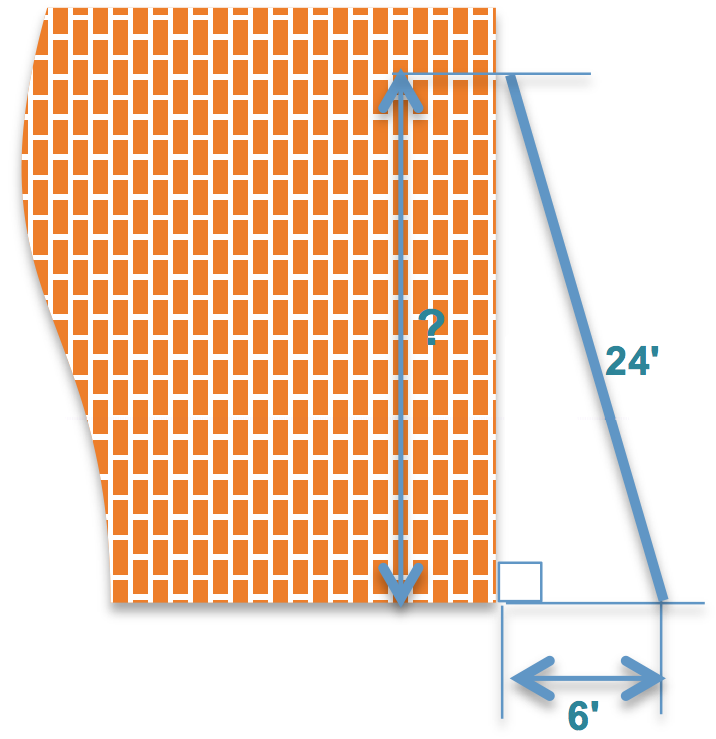
pieds
La bonne réponse est : ANS'
À vous
Longueur d’un hauban
Le mât de l’antenne représentée sur cette figure mesure 18 m de haut, et le hauban est fixé à 1,5 m en-dessous du sommet du mât. Quelle est la longueur du hauban, s’il doit être fixé à 6,5 m de la base du mât de l’antenne ?
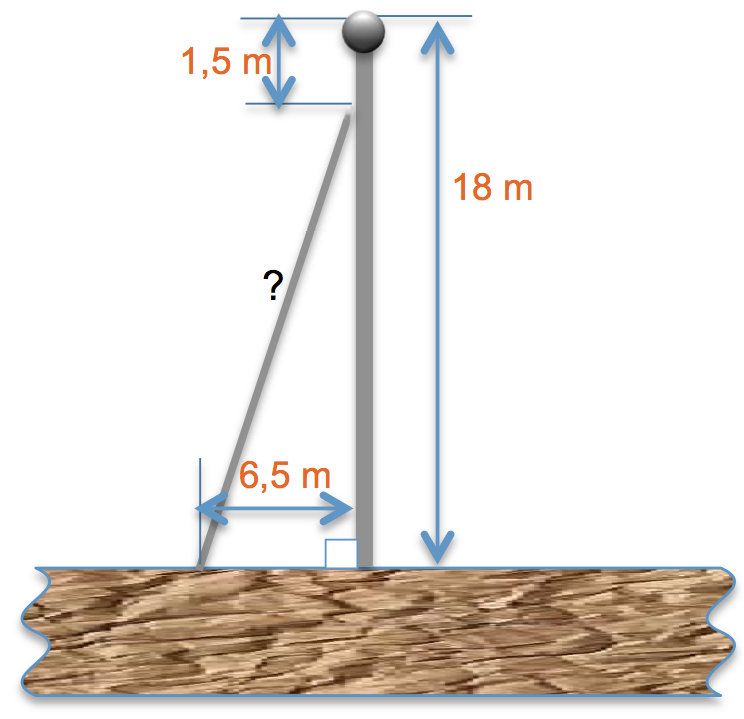
m
La bonne réponse est : ANS m