Rappel
Une fraction est le rapport entre deux nombres entiers :
$$\frac{\class{example1}{\text {nombre de parts utilisées}}}{\class{example2}{\text{nombre de parts disponibles}}}$$
Le nombre de parts utilisées est appelé numérateur, le nombre de parts disponibles est appelé dénominateur.
Exemple
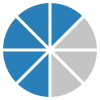
On coupe un gâteau en 8 parts et on en donne 5. Il y a 5 parts utilisées sur 8 parts disponibles.
$$\frac{\class{example1}{5}}{\class{example2}{8}}$$
Trucs et astuces
Utilisez le dollar (1 $) pour mémoriser les fractions !!!
- Le $\frac{1}{2}$ de 1 $ = 50 cents
- Le $\frac{1}{4}$ de 1 $ = 25 cents
- Le $\frac{1}{10}$ de 1 $ = 10 cents
- Le $\frac{1}{20}$ de 1 $ = 5 cents
- Le $\frac{1}{100}$ de 1 $ = 1 cent
Pour additionner ou soustraire deux fractions avec le même dénominateur, faites l’addition ou la soustraction du numérateur et placer le résultat sur le dénominateur.
Pour additionner ou soustraire deux fractions avec un dénominateur différent, trouver le plus petit dénominateur commun voir la leçon : ppdc, convertir les fractions et faire l’addition ou la soustraction du numérateur selon la méthode ci-dessus.
Pour multiplier deux fractions, on multiplie les numérateurs et les dénominateurs. Pour diviser deux fractions, on multiplie par l’inverse de la deuxième fraction.
Exemples
$$\frac{3}{32}+\frac{11}{32}=\frac{14}{32}$$ $$\frac{1}{4}+\frac{4}{16}=\frac{4}{16}+\frac{13}{16}=\frac{17}{16}$$
Attention parce que lorsque l’on mesure il faut aller plus loin que le résultat : on ne peut demander à un électricien de couper un câble électrique à $\frac{17}{16}$ pouces de longueur, voir le ruban à mesurer.
17/16 est une fraction impropre et vous devez la transformer en nombre mixte ou nombre fractionnaire. Une fonction impropre a un numérateur plus grand que le dénominateur.
Pour exprimer une fraction impropre en nombre mixte, on divise le numérateur par le dénominateur :
numérateur | 17 | 16 | dénominateur |
le reste $\Rightarrow$ | 1 | 1 | $\Leftarrow$ c'est le nombre entier |
On prend le reste et on l’exprime avec le même dénominateur que dans la fraction impropre, soit $$\frac{1}{16}$$
On obtient donc $$\frac{17}{16} = 1 \frac{1}{16}$$
À vous
fraction( N1, D1 ) $\times$ fraction( N2, D2 ) = {?}
ANS_N/ANS_DANS_W ANS_N/ANS_D
5
8
2
5
getLCM(D1, D2)
N1 * N2
D1 * D2
getGCF(RAW_N, RAW_D)
RAW_N / GCF
RAW_D / GCF
Math.floor(ANS_N / LCM)
À vous
fraction( N1, D1 ) $\div$ fraction( N2, D2 ) = {?}
ANS_N/ANS_DANS_W ANS_N/ANS_D
5
8
2
5
getLCM(D1, D2)
N1 * D2
D1 * N2
getGCF(RAW_N, RAW_D)
RAW_N / GCF
RAW_D / GCF
UNREDUCED_N % ANS_D
Math.floor(UNREDUCED_N / ANS_D)