Rappel
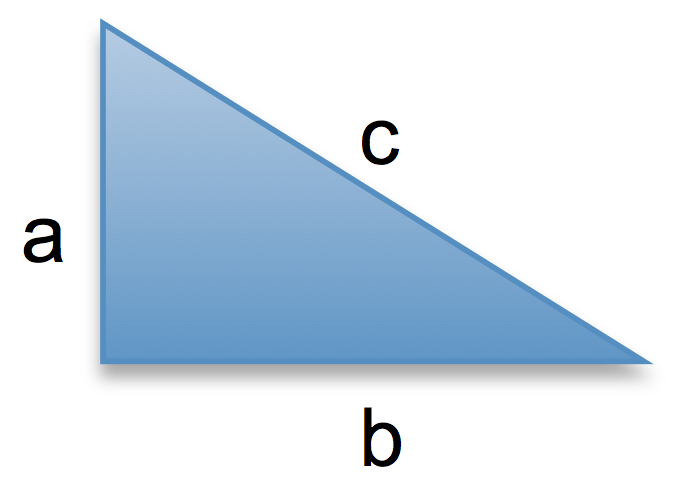
$c^2 = a^2 + b^2$
$a^2 = c^2 – b^2$
$b^2 = c^2 – a^2$
Trucs et astuces
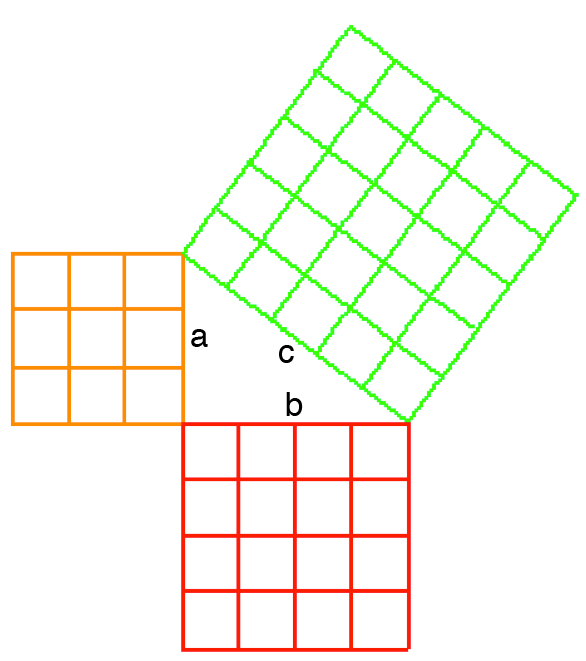
La méthode 3-4-5 est souvent utilisée comme référence par les travailleurs des métiers de la construction. Il s’agit en fait du théorème de Pythagore. Pour démontrer ce théorème, on utilise un triangle droit avec des côtés mesurant 3 pouces, 4 pouces et 5 pouces (ou 3, 4 et 5 pieds ou verges ou toute autre unité).
Si vous multipliez la longueur de chaque petit côté par elle-même et que vous additionnez ces deux résultats, vous obtenez un total représentant la longueur du dernier côté multiplié par lui-même :
$(3 \times 3) + (4 \times 4) = (5 \times 5)\ \text{ou}\ 3^2 \times 4^2 = 5^2$
Donc
| $c^2 = a^2 + b^2$ | $c = \sqrt{a^2 + b^2}$ |
| $a^2 = c^2 - b^2$ | $a = \sqrt{c^2- b^2}$ |
| $b^2 = c^2 - a^2$ | $b = \sqrt{c^2- a^2}$ |
Résolution de problème
- Dessiner un croquis en indiquant les mesures données
- Choisissez la formule à utiliser
- Calculez la réponse
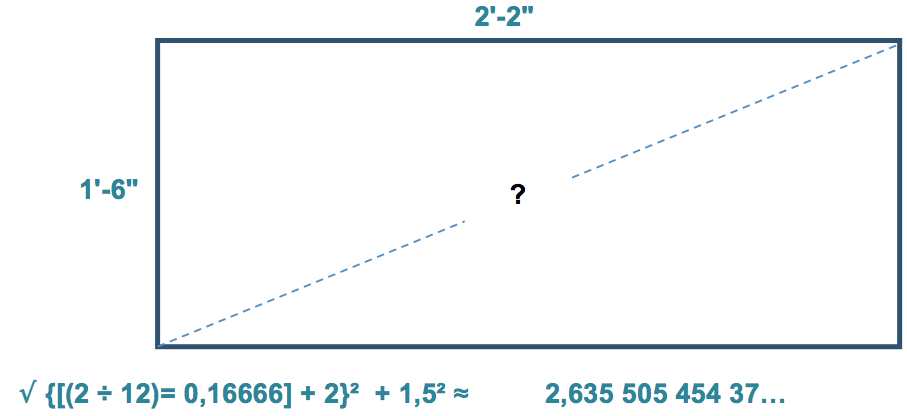
Pour vérifier l’équerrage d’un terrain, on utilise le calcul trigonométrique de la diagonale :
Donc : $\sqrt{2,167^2 + 1,5^2} ≈ 2,636'$
Soit : $2'\text{-}7 \frac{5}{8}''$
À vous
Diagonale de la fixation en acier
Calculez la diagonale de la fixation en acier illustrée ci-contre.

cm
Donc : $\sqrt{4^2 + 2\text{,}5^2} ≈ 4\text{,}716\ 990\ 566\text{ soit }4\text{,}717\text{ cm}$
La bonne réponse est : ANS
À vous
Aire de deux pièces en acier galvanisé à souder
Deux pièces en acier galvanisé ont la forme et les dimensions suivantes : un demi cercle dont le diamètre représente la diagonale du triangle et le triangle rectangle a une longueur de 8 cm et une largeur de 6 cm.
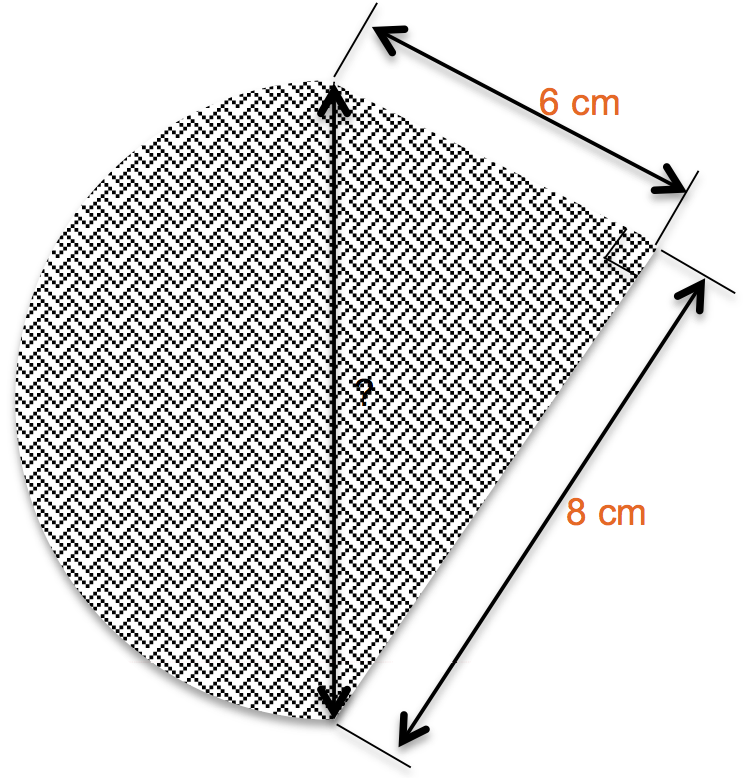
Calculez la surface totale des deux pièces une fois soudées.
cm2
Donc: $\sqrt{6^2 + 8^2} = 10$
Le diamètre du disque est donc de 10 cm et l’aire du triangle sera la moitié de l’aire du rectangle de 6 cm par 8 cm.
Calcul de l’aire du demi disque : [(d÷2)2 x π] ÷ 2 = [(10 ÷ 2)2 x π] ÷ 2 ≈ 39,269 908 169 9... ou 39,270 cm2
Calcul de l’aire du triangle : (L x l) ÷ 2 = (8 x 6) ÷ 2 = 24 cm2
Surface totale de la pièce en aluminium : 39,270 + 24 = 63,270 cm2
La bonne réponse est : ANS cm2.