À vous
Calcul trigonométrique
4 points
Pour trouver le centre du garage où creuser le drain, on calcule la diagonale et on divise cette longueur par deux.
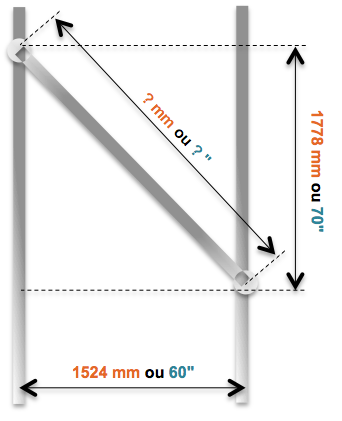
Selon le schéma suivant, il faut souder une pièce de renfort entre les deux barres parallèles. Calculez la longueur de la pièce de renfort en millimètres et en pouces.
Truc : la méthode 3-4-5
mm
La bonne réponse est : ANS m
1. Calcul trigonométrique (2 points par bonne réponse)
$a^2 + b^2 = c^2$ et $c = \sqrt{(a^2 + b^2)}$
$c^2 - b^2 = a^2$ et $a = \sqrt{(c^2 - b^2)}$
$c^2 - a^2 = b^2$ et $b = \sqrt{(c^2 - a^2)}$
$\sqrt{(1\ 778^2 + 1\ 524^2)} ≈ \sqrt{5\ 483\ 860} ≈ 2\ 341\text{,}764\ 292\ 15$ ...soit 2 341,764 mm
Quelle distance en mètres parcourez-vous en 2 secondes à 80 km/h (sur route) ?
m
La bonne réponse est : ANS m
Mesures en pouces :
$\sqrt{70^2 + 60^2} = \sqrt{8\ 500 ≈ 92\text{,}195\ 444\ 572}$...soit 92,195" arrondi au millième ou 92 3/16" sur le ruban à mesurer.
Utilisation de formules et résolution de problèmes
2 points par exercice

a. Calculez l’intensité de soudure selon la formule du module Fonction, formules et problèmes pour les électrodes de diamètres suivants :
Ø = 1,6
A
La bonne réponse est : ANS A
50 x (1,6 - 1) = 30 A
Ø = 5
A
La bonne réponse est : ANS A
50 x (5 - 1) = 200 A
Ø = 6,3
A
La bonne réponse est : ANS A
50 x (6,3 - 1) = 265 A
Tension de la soudure
b. Calculez la tension de la soudure selon la formule du module Fonction, formules et problèmes pour les électrodes de mêmes diamètres.
Ø = 1,6
VLa bonne réponse est : ANS V
20 + (0,04 x 30) = 21,2 V
Ø = 5
VLa bonne réponse est : ANS V
20 + (0,04 x 200) = 28 V
Ø = 6,3
VLa bonne réponse est : ANS V
20 + (0,04 x 265) = 30,6 V
Calcul de l’énergie de soudure
c. Calculez l’énergie de soudure (heat input) selon la formule du module Fonction, formules et problèmes pour les électrodes de mêmes diamètres pour une soudure à l’arc avec électrode enrobée avec une vitesse d’avance Vs :
- Vs = 20 cm/min pour le diamètre de 1,6 mm
- Vs = 35 cm/min pour le diamètre de 5 mm
- Vs = 45 cm/min pour le diamètre de 6,3 mm
Électrode Ø 1,6
kJLa bonne réponse est : ANS kJ
$\large{\frac{60 \times 21\text{,}2 \times 30}{1\ 000 \times 20}} \normalsize= 1,908\text{ kJ}$
Électrode Ø 5
kJLa bonne réponse est : ANS kJ
$\large{\frac{60 \times 28 \times 200}{1 000 \times 35}} \normalsize= 9\text{,}6 \text{ kJ}$
Électrode Ø 6,3
kJLa bonne réponse est : ANS kJ
$\large{\frac{60 \times 30\text{,}6 \times 265}{1\ 000 \times 45}} \normalsize= 10\text{,}812 \text{ kJ}$