Rappel

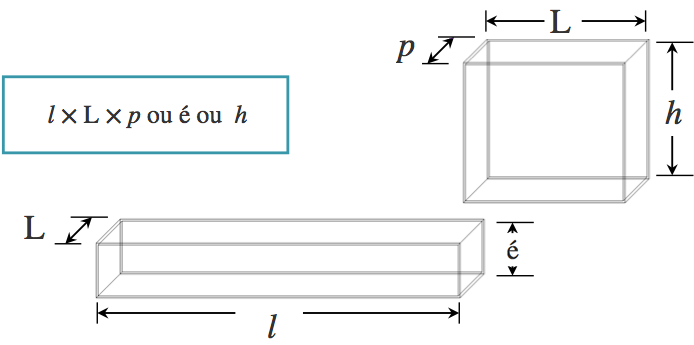
Pour calculer le volume $V$, on multiplie les trois mesures suivants :

  • Hauteur : $h$
  • Largeur : $\text{L}$
  • Profondeur : $p$
  • Longueur : $l$
  • Largeur : $\text{L}$
  • Épaisseur : $é$
  • Hauteur : $h$
  • Diamètre : $d\ ou\ Ø$
  • Rayon : $r$

Trucs et astuces

Le calcul des volumes adopté en industrie est effectué en arrondissant précisément à la troisième décimale près et n’arrondissez pas pendant les calculs, seulement pour le résultat !

Exemple

a. L'excavation

Pour calculer le volume de terre excavée pour la maison, on multiplie la longueur ($l$) par la Largeur $(\text{L})$ par la hauteur $(h)$.

Remarque

Il importe d’exprimer les calculs en mètre cube (m3), vous verrez pourquoi un peu plus tard.

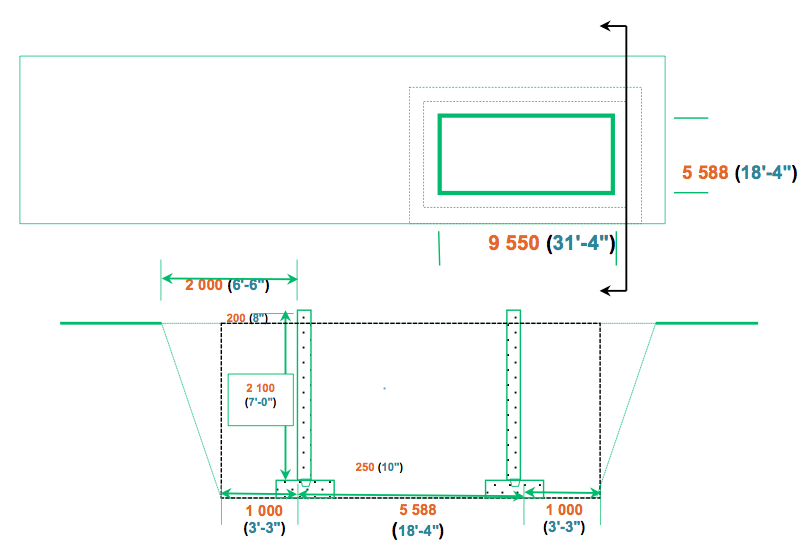
Schéma vu du dessus du terrain, du bâtiment et du volume de terre à excaver avec les dimensions du bâtiment. Schéma coupe du volume de terre à excaver pour calculer le volume du béton des murs de fondation.

Soit :
$1\,000 + 5\,588 + 1\,000 = \class{example2}{7\,588}$
$1\,000 + 9\,550 + 1\,000 = \class{example2}{11\,550}$
Alors :
$7\,588 \times 11\,550 \times (2\,100 - 200) = 166\,518\,660\,000\,\text{mm}^3$
$7\,588 \times 11\,550 \times (2\,100 + 250) = 205\,957\,290\,000\,\text{mm}^3$
Alors :
$7\,588 \times 11\,550 \times (2\,100 - 200) = 166\,518\,660\,000\,\text{mm}^3$
$7\,588 \times 11\,550 \times (2\,100 + 250) = 205\,957\,290\,000\,\text{mm}^3$

Remarques

Il ne suffit pas d’enlever la hauteur du débordement à la hauteur du mur de fondation, il faut également ajouter la hauteur de l’empattement.

Il ne suffit pas d’ajouter la hauteur de l’empattement, il faut également enlever la hauteur du débordement à la hauteur du mur.

De plus, pour ne pas avoir de chiffres trop longs à calculer, convertissez vos mesures en mètre :

$7\text{,}588 \times 11\text{,}55 \times (2\text{,}1 - 0\text{,}2 + 0\text{,}25) = 7\text{,}588 \times 11\text{,}55 \times \class{example2}{2\text{,}15} = \class{example2}{188\text{,}429\,\text{m}^3}$

Vous aurez donc $189\ \text{m}^3$ de terre à excaver sans tenir compte de la pente obligatoire qui doit aussi être excavée pour prévenir les glissements de terrain et assurer la protection des travailleurs.

En pouce, cela donne :
$3'\text{-}3'' + 18'\text{-}4'' + 3'\text{-}3'' = 24'-10''$
$3'\text{-}3'' + 31'\text{-}4'' + 3'\text{-}3'' = 37'-10''$

Alors :
$24'\text{-}10'' \times 37'\text{-}10'' \times (7'\text{-}0''-8') =\ ???$
$24\text{,}833 \times 37\text{,}833 \times (7'\text{-}0''-8' = 10'') = 24,833 \times 37\text{,}833 \times \class{example1}{\bf{7\text{,}167}} = \class{example1}{\bf{6\,733\text{,}446\ \text{pi}^3}}$
ou $6\,733\text{,}446 ÷ 27 = \class{example1}{\bf{249\text{,}387\ \text{v}^3}}$

Vous aurez donc $\bf250\ \text{v}^3$ de terre à excaver.

À vous

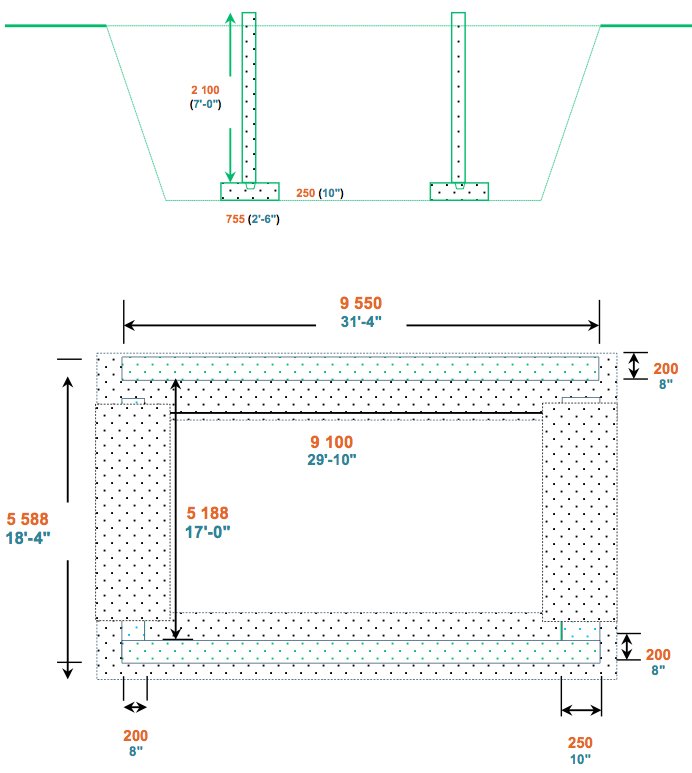
Schéma du mur de fondation vu du dessus avec les mesures en millimètres et en pieds et pouces.

Calculer le volume du béton entrant dans les murs de fondation en m3
{?} m3

[(9 550 × 2) + 5 188] × 2,100 × 200 + (5 188 × 2 100 × 250) = 12,293 m3

La bonne réponse est ANS (ANS_CEIL).

12.293 globals.frenchFormatNumber(ANS_R) Math.ceil(12.293) ANS_R_CEIL.toString().split('.').join(',')

Remarque

Vous vous souvenez, dans l’exemple, une remarque vous suggérait de faire vos calculs de volume en système métrique. Voici pourquoi.

{[(31'-4" × 2) + 17'-0"] × 7'-0" × 8"} + (17'-0" × 7'-0" × 10" = 470,92 pi3 ou

470,92 pi3 ÷ 27 = 17,45 v3 ou 470,92 pi3 ÷ 35,28 = 13,35 m3

Vous aurez donc besoin de 13,35 m3 pour couler ces murs de fondation.

On note que, par convention, on divise par 35,28 pour passer des pieds cubes aux mètres cubes. Le résultat obtenu n’est donc pas tout à fait identique. Pour cette raison, vous utiliserez de préférence les mesures métriques pour calculer les volumes.