Partie 1
Périmètre (1 dimension)
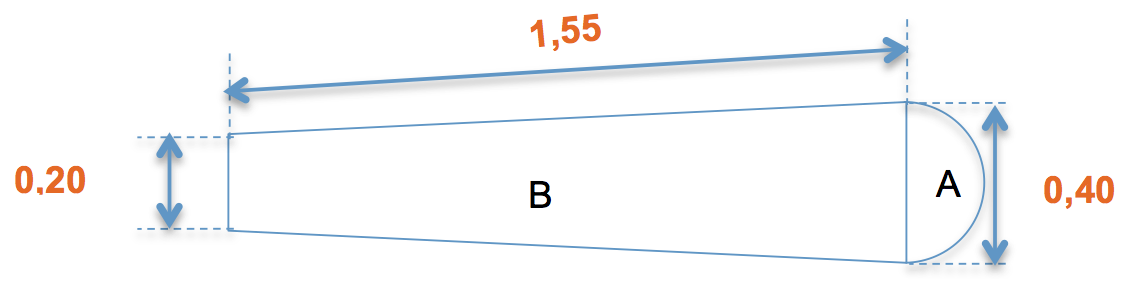
Un particulier décide d’installer une éolienne dans son jardin pour alimenter la pompe de sa piscine. L’éolienne dispose de trois pales de dimensions identiques (voir le schéma ci-dessous). Quel est le périmètre d’une pale ?
B est un trapèze. A est un demi cercle.
Rappel
Pour calculer le périmètre d’un trapèze, on ajoute les 4 côtés.
À vous
Quel est le périmètre de la pale ?
{?} m
3.928
Donc : On calcule le périmètre du cercle qu’on divise par deux.
0,40 x π ÷ 2 = 0,628 318 530 71 m ou 0,628 arrondi au millième.
Puis On calcule le périmètre du trapèze.
0,20 + 1,55 + 0,40 + 1,55 = 3,70 m
Et On ajoute les deux. Mais n’oubliez pas d’enlever la base la plus large du trapèze ! 3,70 - 0,40 + 0,628 = globals.frenchFormatNumber(ANS_R) m.
La bonne réponse est globals.frenchFormatNumber(ANS_R) m.
Partie 2
Surface ou aire (2 dimensions)
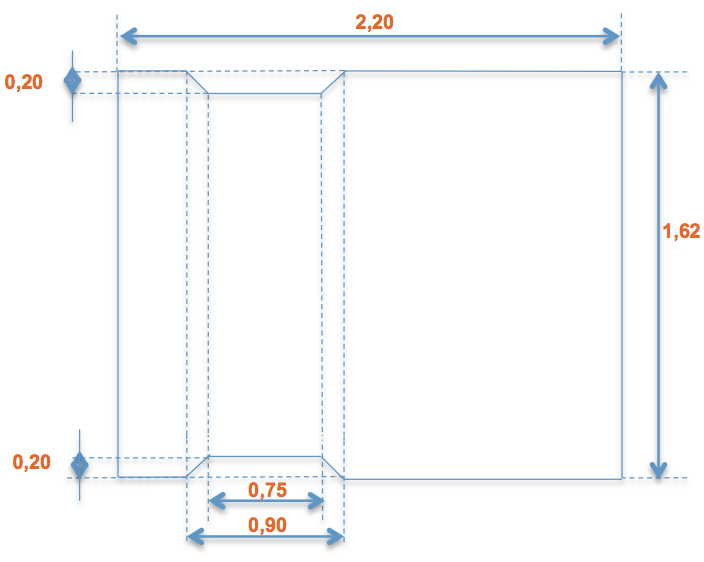
Un entrepreneur décide de protéger le sol de son fourgon à l’aide d’un plancher (voir le plan ci-dessous). La partie surélevée correspond au passage des roues arrière du fourgon.
Rappel
Pour calculer l’aire d’un trapèze (deux bases parallèles) on multiplie la somme de ses deux bases par la hauteur et on divise par le tout 2 :
[(petite base + grande base) x hauteur] ÷ 2 = Aire du trapèze.
À vous
Quelle est la surface du plancher ?
(Voir le plan ci-dessus.)
{?} m2
3.234
Donc : On calcule d’abord la surface totale. 2,20 x 1,62 = 3,564 m2
2,20 x 1,62 = 3,564 m2
Ensuite, on calcule le passage des roues (0,75 + 0,90) x 0,20 ÷ 2 = 0,165 m2
Puis on enlève deux fois le passage des roues du total. 3,564 – (0,165 x 2) = 3,234 m2
La bonne réponse est globals.frenchFormatNumber(ANS_R) m2.