Rappel

Pour calculer le volume $V$, on multiplie les trois mesures suivants :

  • Hauteur : $h$
  • Largeur : $\text{L}$
  • Profondeur : $p$
  • Longueur : $l$
  • Largeur : $\text{L}$
  • Épaisseur : $é$
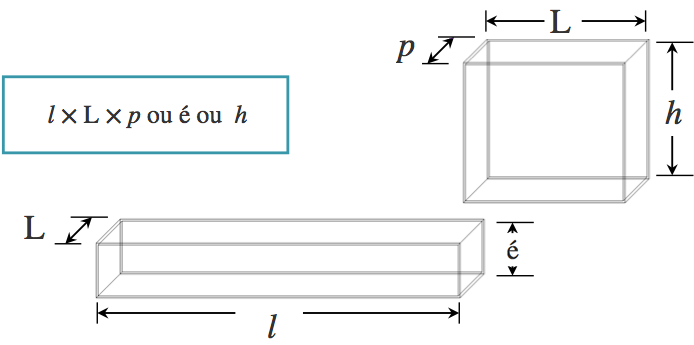
  • Hauteur : $h$
  • Diamètre : $d\ ou\ Ø$
  • Rayon : $r$

Trucs et astuces

Le calcul des volumes adopté en industrie est effectué en arrondissant précisément à la troisième décimale près et n’arrondissez pas pendant les calculs, seulement pour le résultat !

Exemple

Enseigne de sortie

Pour calculer le volume de cette enseigne de sortie en centimètres cubes ou en pouces cubes, il faut calculer la longueur par la hauteur par la profondeur.

  • Longueur : 12" ou 304,8 mm
  • Hauteur : 8" ou 203,2 mm
  • Profondeur : 1 1/4" ou 31,75 mm
Schéma d’une enseigne de sortie avec une longueur de 12'' ou 304,8 mm, une hauteur de 8'' ou 203,2 mm et une profondeur de 1 1/4'' ou 31,75 mm.

Remarque

La conversion des pouces en centimètres ne donne pas des mesures précises (centièmes de millimètres). Pour de gros volumes (mètre cube), l’imprécision devient problématique.

Pour ne pas avoir de chiffres trop longs à calculer, convertissez vos mesures en centimètres.

Donc :
304,8 mm x 203,2 mm x 31,75 mm =
30,48 cm x20,3 cm x 3,175 cm =
1 966,447 68 cm3 ou 1 966,447cm3 arrondi au millième.

En pouce, cela donne :
12" x 8" x 1,25" = 120 po3

1 po3 ≈ 16,387 064 cm3, soit 120 x 16,387 064 =
1 966,447 68 cm3 ou 1 966,447 cm3 arrondi au millième.

À vous

Une conduite a un diamètre de 152,4 mm (6") et une longueur de 3,657 6 m (12') de long. Si vous bouchez une des extrémités, quel volume d’eau en litres peut contenir cette conduite ?


Schéma d’une conduite d’un diamètre de 152,4 mm (6'') et d’une longueur de 3,657 6 m (12') de long.


{?} litres

(152,4 mm ÷ 2)2 x 3,6576 m x π = ?

Trucs et astuces :
convertissez toutes les mesures dans la même unité.
152,4 mm = 0,152 4 m
(0,1524 m ÷ 2)2 x 3,657 6m x π ≈
0,005 805 44 x 3,6576 m x π ≈
0,066 771 995 7m3

Remarque :
1 m3 = 1000 l
Donc 66,771 995 7 l ou 66,772 l arrondi au millième

La bonne réponse est ANS l.

66.772 globals.frenchFormatNumber(ANS_R)

Remarque

Utiliser les mesures métriques pour calculer les volumes

Pourquoi ?

Une conduite a un diamètre de 152,4 mm (6") et une longueur de 3,657 6 m (12') de long. Si vous bouchez une des extrémités, quel volume d’eau en gallons peut contenir cette conduite ?

En pouce, cela donne :
(6" ÷ 2)2 x 12' x π = ?
6" = 6/12' = 1⁄2' ou 0,5'
(0,5' ÷ 2)2 x 12' x π ≈ 2,356 193 03 pi3

Remarque :
1 pi3 = 6,2288355 gal
Donc 14,676 339 gal ou 14,676 gal arrondi au millième

Remarque :
1 gal = 4,546 09 l
14,676 gal ≈ 66,718 417 l

Le résultat obtenu n’est donc pas tout à fait identique. Il a plus de 1⁄2 l ou 2 tasses 1⁄4 d’écart.
Pour cette raison, vous utiliserez de préférence les mesures métriques pour calculer les volumes.