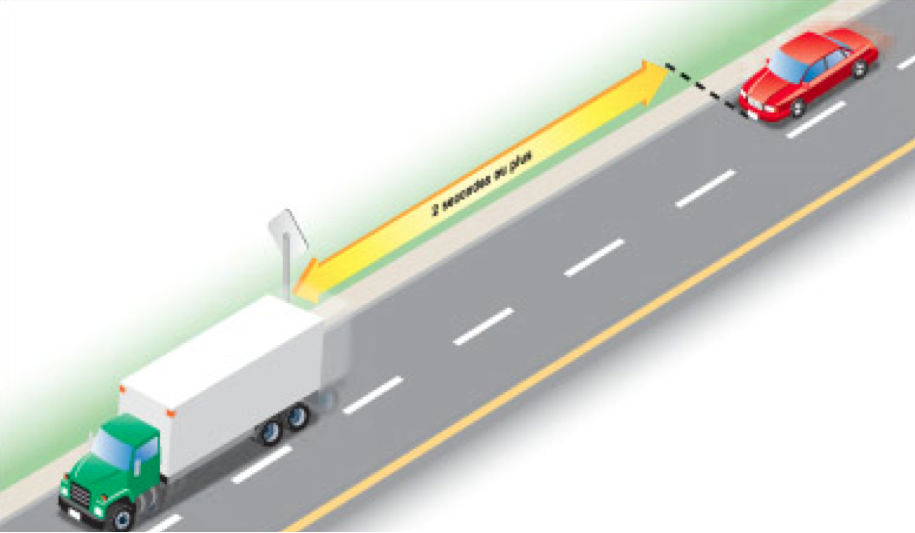
Distance de sécurité
La distance de sécurité entre deux véhicules est donnée par la formule :
D = 0,6 x v
D est la distance de sécurité en mètre (m).
v est la vitesse de la voiture en kilomètre par heure (km/h).
Calculez la distance de sécurité si la vitesse est 80 km/h.
m
La bonne réponse est : ANS m.
À vous
Une voiture roule à 57 m d’une autre. Quelle devrait être sa vitesse maximum pour respecter la distance de sécurité ?
0,6 x v = 57 m
km/h
Donc 57 ÷ 0,6 = 95 km/h
La bonne réponse est : ANS km/h
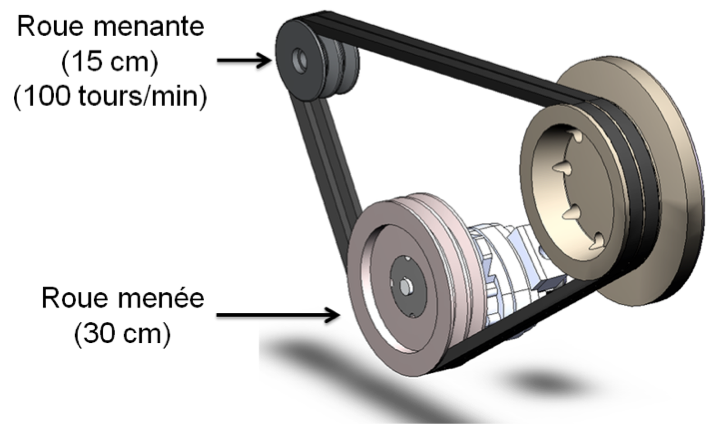
Ratio d’entraînement
Dans les pignons dentés ou les poulies, le ratio d’entraînement de l’engrenage mené sur l’engrenage menant se calcule en divisant la vitesse, le nombre de dents ou le diamètre de la roue menée (en tours par minute) par la vitesse, le nombre de dents ou le diamètre de la roue menante. Le ratio est donné par cette formule :
$R = \frac{D_1}{D_2} = \frac{V_1}{V_2}$ ou $R = \frac{Z_1}{Z_2} = \frac{V_1}{V_2}$
- $\color{red}{D_1}$ est le diamètre de la roue entraînée ou menée
- $\color{green}{D_2}$ est le diamètre de la roue entraînante ou menante
- $\color{red}{Z_1}$ est le nombre de dents de la roue entraînée (ou du pignon)
- $\color{green}{Z_2}$ est le nombre de dents de la roue entraînante (ou du pignon)
- $\color{red}{V_1}$ est la vitesse de la roue menée
- $\color{green}{V_2}$ est la vitesse de la roue menante
- $R$ est le ratio

Règles
ATTENTION, les unités doivent être identiques ! Si $\color{red}{D_1}$ est donné en millimètres et $\color{green}{D_2}$ en centimètres, on doit convertir les mesures dans la même unité ! En général on exprime les ratios d’entraînement sous la forme x:1
Exemple
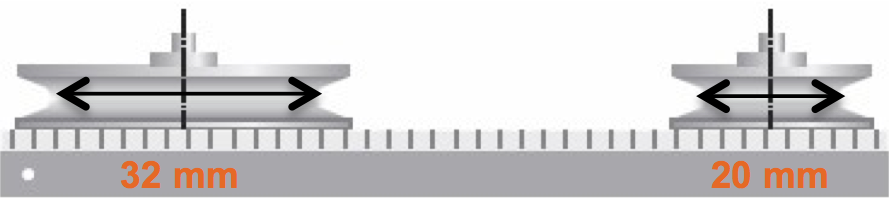
Quel est le ratio d’entraînement si la poulie menée mesure 20 mm de diamètre et la poulie menante en mesure 32 mm ?
$\color{red}{D_1} = 20$
$\color{green}{D_2} = 32$
$R = 20 ÷ 32 = 5 ÷ 8 = 0\text{,}625$
qu’on peut écrire 0,625:1
À vous
Quel est le ratio d’entraînement si la vitesse de la roue menée est de 60 tours par minute et la vitesse de la roue d’entraînement est de 160 tours par minute ?
$\color{red}{V_1} = 60$
$\color{green}{V_2} = 160$
$R = $ ?:1
Le ratio R =
:1
R = 60 ÷ 160 = 3 ÷ 8 = 0,375 qu’on peut écrire 0,375
La bonne réponse est : ANS.