1. Périmètre (1 dimension)
Exemple a
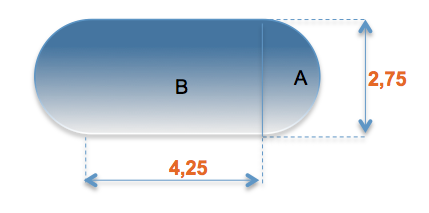
Un plombier doit raccorder un réservoir dont les extrémités sont semi-circulaires. Le fond est illustré ci-dessous. Quel est le périmètre de la base du réservoir ?
B est un rectangle. A est un demi cercle.
À vous
Quel est le périmètre de la clôture ?
m
La bonne réponse est : ANS m
Donc :
On calcule le périmètre du cercle (2 x π x r).
2,75 x π = 8,639 379 797 37 m ou 8,639 arrondi au millième.
Puis
On ajoute 2 fois la longueur du rectangle.
4,25 + 4,25 = 8,50 m
Et
On ajoute les deux.
8,50 + 8,639 = 17,139 m
2. Surface ou aire (2 dimensions)
Exemple b
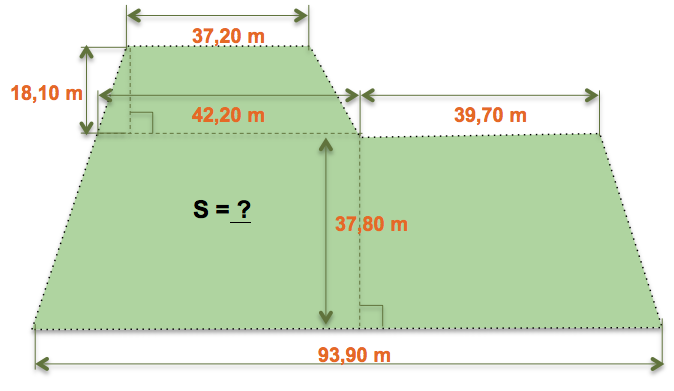
Un voisin fait clôturer son terrain selon le plan suivant. Quelle est la surface du terrain en mètres carrés ?
Rappel
Pour calculer l’aire d’un trapèze (deux bases parallèles) on utilise la formule suivante :
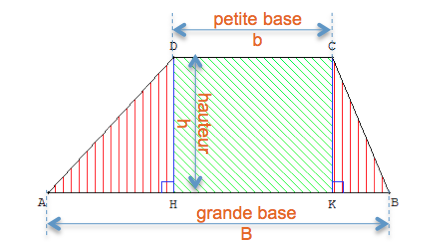
Source de l’image : DEBART P. (2008). « Aires du parallélogramme et du trapèze » : http://debart.pagesperso-orange.fr/college/aire_parallelogramme.html#ch2 (page consultée en mars 2015)
À vous
Quelle est la surface du terrain en mètres carrés ?
{?} m2
4041.24
Donc :
On calcule d’abord la surface du grand trapèze.
Petite base = 42,20 + 39,70 = 81,90 m
$$\text{S} = \frac{37\text{,}80(93\text{,}90 + 81\text{,}90)}{2}= 37\text{,}80 \times 87\text{,}90 = 3\ 322\text{,}62 \text{m}^2$$
Ensuite, on calcule la surface du petit trapèze.
$$\text{S} = 18\text{,}10 \frac{(42\text{,}20 + 37\text{,}20)}{2} = 18\text{,}10 \times 39\text{,}70 = 718\text{,}57 \text{m}^2$$
Puis on ajoute les deux surfaces.
3 322,62 + 718,62 = 4 041,24 m2
La bonne réponse est : globals.frenchFormatNumber(ANS_R) m2.