Rappel
La racine carrée d’un nombre réel positif x est le nombre qui, lorsqu’il est multiplié par lui-même, donne x. On écrit √x ou x1/2 et x est le radicande, √ est le radical. Si la racine carrée est un nombre entier, on dit que le carré est parfait.
Exemples :
3 est la racine carrée de 9 car 3 x 3 = 9 ou 32 = 9
√100 = 10 car 10 x 10 = 100 ou 102 = 100
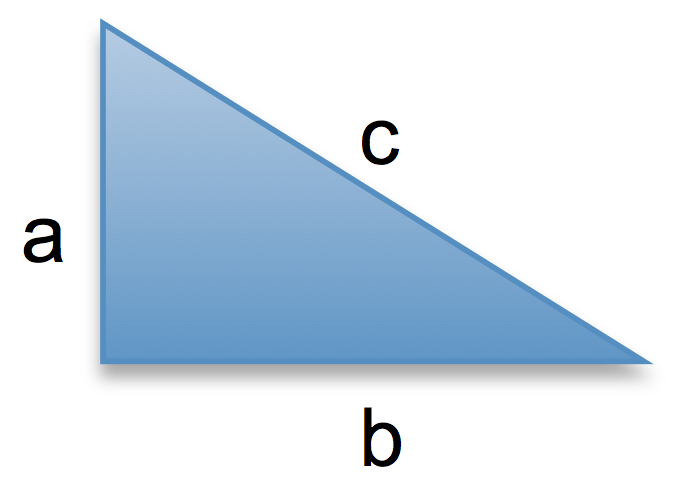
$c^2 = a^2 + b^2$
$a^2 = c^2 – b^2$
$b^2 = c^2 – a^2$
Trucs et astuces
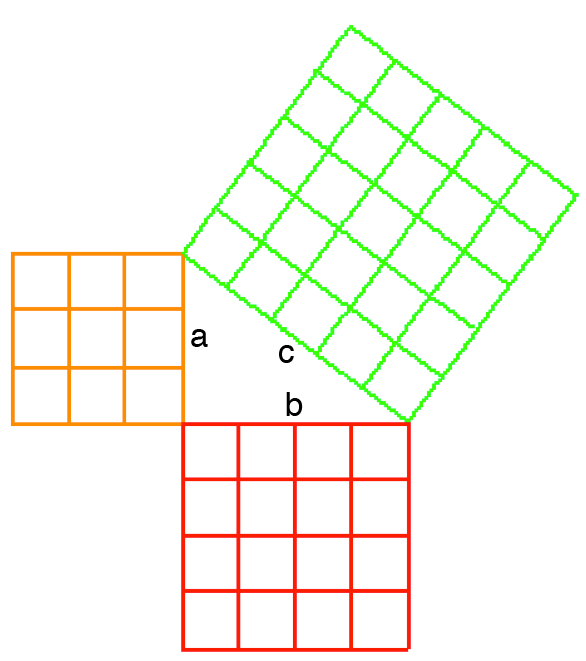
La méthode 3-4-5 est souvent utilisée comme référence par les travailleurs des métiers de la construction. Il s’agit en fait du théorème de Pythagore. Pour démontrer ce théorème, on utilise un triangle droit avec des côtés mesurant 3 pouces, 4 pouces et 5 pouces (ou 3, 4 et 5 pieds ou verges ou toute autre unité).
Si vous multipliez la longueur de chaque petit côté par elle-même et que vous additionnez ces deux résultats, vous obtenez un total représentant la longueur du dernier côté multiplié par lui-même :
$(3 \times 3) + (4 \times 4) = (5 \times 5)\ \text{ou}\ 3^2 \times 4^2 = 5^2$
Donc
| $c^2 = a^2 + b^2$ | $c = \sqrt{a^2 + b^2}$ |
| $a^2 = c^2 - b^2$ | $a = \sqrt{c^2- b^2}$ |
| $b^2 = c^2 - a^2$ | $b = \sqrt{c^2- a^2}$ |
Résolution de problème
- Dessiner un croquis en indiquant les mesures données
- Choisissez la formule à utiliser
- Calculez la réponse
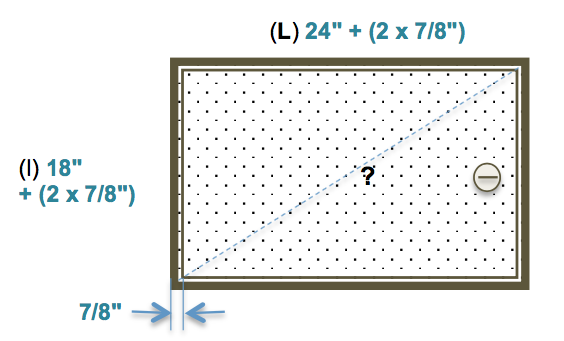
Pour placer une trappe d’accès à la plomberie d’une baignoire de 18" par 24", on perce un trou dans un panneau de gypse. On laisse un espace de 7/8" de chaque côté pour le cadre. Pour vérifier l’équerrage du trou découpé, on utilise le calcul trigonométrique de la diagonale :
$\sqrt{(24+(2\times7/8))^2+(18+(2\times7/8))^2} ≈ 32\text{,}451887464$
Donc : $\sqrt{25\text{,}75^2 + 19\text{,}75^2} ≈ 32\text{,}452\text{"}$ arrondi au millième
À vous
Échelle
Un plombier utilise l’échelle de vingt pieds ci-contre pour remplacer l’évent de l’extracteur de la salle de bain sur son toit. Le bas de l'échelle ne peut pas être à plus de cinq pieds de l’immeuble. Quelle est la hauteur minimale à laquelle l’échelle sera en contact avec le bâtiment ?
pi
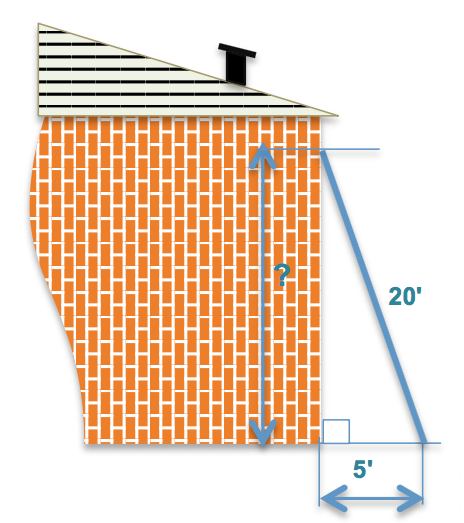
Donc : $\sqrt{(20^2 - 5^2 )} ≈ 19\text{,}364\ 916\ 731$
La bonne réponse est : ANS pi.
À vous
Longueur d’un tuyau
La plomberie d’une maison comporte une installation enterrée à l’extérieur avec un tuyau de relevage pour atteindre les égouts selon le schéma suivant. Quelle est la hauteur entre la sortie de la station et le raccordement à l’égout ?
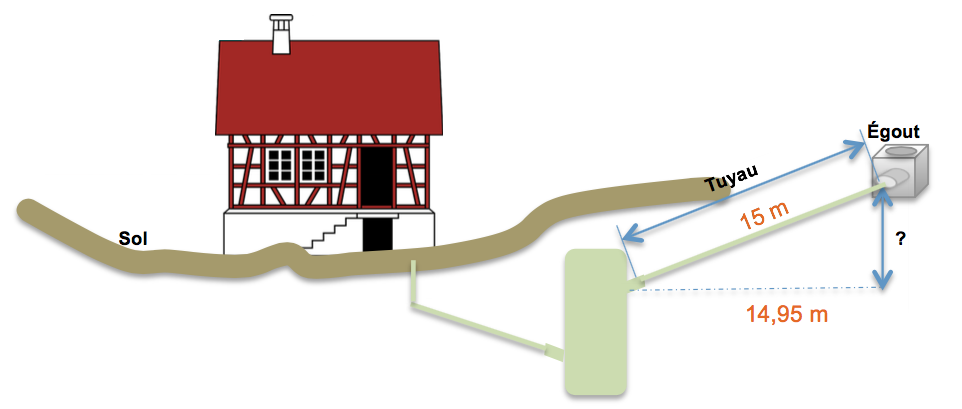
m
Donc $\sqrt{(15^2 - 14\text{,}95^2)} ≈ 1\text{,}223\ 723\ 825$
La bonne réponse est : ANS m.