Rappel

Dans certaines applications pratiques en soudure, vous rencontrerez des fractions impropres et des nombres mixtes surtout en calculant dans le système impérial.

Exemple

Fractions impropres

Une fraction impropre est une fraction dont le numérateur est plus grand que le dénominateur.

$$\frac{15}{4}$$
$$\frac{8}{3}$$
$$\frac{3}{2}$$
$$\frac{21}{5}$$

Nombres mixtes

Un nombre mixte est une fraction accompagnée d’une valeur entière.

$$3\frac{3}{4}$$
$$2\frac{1}{3}$$
$$1\frac{1}{2}$$
$$5\frac{1}{5}$$

Trucs et astuces 1

Pour calculer, on peut choisir de transformer les nombres mixtes en fractions impropres. Pour cela, on multiplie la partie entière par le dénominateur, on ajoute le numérateur et on place le tout sur le dénominateur.

Exemple

$$\class{example1}{3}\frac{\class{example2}{1}}{\class{example3}{4}}$$
  • La partie entière : 3
  • Le numérateur : 1
  • Le dénominateur : 4

Donc : $$ \class{example1}{3}\frac{\class{example2}{1}}{\class{example3}{4}} = \frac{\class{example1}{3} \times \class{example3}{4}}{\class{example3}{\class{example3}{4}}} + \frac{\class{example2}{1}}{\class{example3}{4}} = \frac{\class{example1}{3} \times \class{example3}{4} + \class{example2}{1}}{\class{example3}{4}} = \frac{13}{\class{example3}{4}} $$

Quand on additionne, soustrait, multiplie ou divise avec des nombres mixtes transformés en fractions impropres, au résultat on peut revenir à un nombre mixte. Pour cela, on divise le numérateur par le dénominateur jusqu’à obtenir un premier reste. Le résultat est la partie entière et on place le reste sur le numérateur pour obtenir la partie fractionnaire.

Exemple

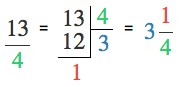
Trucs et astuces 2

Pour calculer on peut aussi choisir de transformer les nombres mixtes en nombres décimaux. Pour cela on isole d’abord la partie entière, puis on convertit la partie fractionnaire en nombre décimal.

Exemple

$$\class{example1}{3}\class{example2}{\frac{1}{4}}$$
  • La partie entière : 3
  • La partie fractionnaire : $\frac{1}{4}$
  • Le nombre décimal : $0\text{,}25$
$$\class{example1}{3} \class{example2}{\frac{1}{4}} = \class{example1}{3} + \class{example2}{\frac{1}{4}} =$$ $$\class{example1}{3} + (\class{example2}{1} \div \class{example2}{4}) = \class{example1}{3} + \class{example3}{0\text{,}25} =$$

Donc :

$$\text{ }\class{example1}{3} \class{example2}{\frac{1}{4}} = 3\text{,}25$$

Attention

Tous les nombres mixtes ne peuvent pas être transformés en nombres décimaux. Parfois la fraction donne une décimale périodique.

Exemples

2/3 = 2 ÷ 3 = 0,666…

1/11 = 1 ÷ 11 = 0,090909…

À vous

Une barre plate en acier a été coupée en 5 tronçons de 3 1/2", 4 5/8", 6 3/4", 7 1/2" et 8 1/4". La perte est 1/16" à chaque coupe et il n’y a aucun reste. Combien mesurait la barre ?

{?} pouces
La bonne réponse est : ANS_STR".

Donc il y a 4 fois 1/16" de perte, plus tous les tronçons, soit :

$$3\frac{1}{2} + 4\frac{5}{8} + 6\frac{3}{4} + 7\frac{1}{2} + 8\frac{1}{4} + (4 \times \frac{1}{16}) =$$ $$\frac{(3 \times 2) + 1}{2} + \frac{(4 \times 8) + 5}{8} + \frac{(6 \times 4) + 3}{4} + \frac{(7 \times 2) + 1}{2} + \frac{(8 \times 4) + 1}{4} + \frac{(4 \times 1)}{16} =$$ $$\frac{7}{2} + \frac{37}{8} + \frac{27}{4} + \frac{15}{2} + \frac{33}{4} + \frac{4}{16}$$

On cherche le plus petit commun multiple : ici c’est 16. Ensuite, on procède comme on l’a vu dans la partie Plus petit commun multiple (PPCM) – Plus petit dénominateur commun (PPDC).

$$\frac{7 \times 8}{2 \times 8} + \frac{37 \times 2}{8 \times 2} + \frac{27 \times 4}{4 \times 4} + \frac{15 \times 8}{2 \times 8} + \frac{33 \times 4}{4 \times 4} + \frac{4}{16} =$$ $$\frac{56}{16} + \frac{74}{16} + \frac{108}{16} + \frac{120}{16} + \frac{132}{16} + \frac{4}{16} =$$ $$\frac{56 + 74 + 108 + 120 + 132 + 4}{16} =$$ $$\frac{494}{16}$$

On obtient une fraction impropre que l’on transforme en nombre mixte :

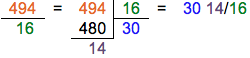
On simplifie pour obtenir 30" 7/8

Remarque : Pour simplifier le calcul, on peut additionner les parties entières d’un côté et les parties fractionnaires de l’autre :

$$3 + 4 + 6 + 7 + 8 + \frac{1}{2} + \frac{5}{8} + \frac{3}{4} + \frac{1}{2} + \frac{1}{4} + \frac{(4 \times 1)}{16} =$$ $$28 + \frac{1}{2} + \frac{5}{8} + \frac{3}{4} + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} =$$

On cherche le plus petit commun multiple : ici c’est 8. Ensuite, on procède comme on l’a vu dans la partie Plus petit commun multiple (PPCM) – Plus petit dénominateur commun (PPDC).

$$28 + \frac{1}{2} + \frac{5}{8} + \frac{3}{4} + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} =$$ $$28 + \frac{1 \times 4}{2 \times 4} + \frac{5}{8} + \frac{3 \times 2}{4 \times 2} + \frac{1 \times 4}{2 \times 4} + \frac{1 \times 2}{4 \times 2} + \frac{1 \times 2}{4 \times 2} =$$ $$28+ \frac{4}{8} + \frac{5}{8} + \frac{6}{8} + \frac{4}{8} + \frac{2}{8} + \frac{2}{8} =$$ $$28+ \frac{4 + 5 + 6 + 4 + 2 + 2}{16} = 28 + \frac{23}{8}$$

On transforme la fraction impropre en nombre mixte :

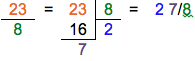
On ajoute ce résultat à 28, ce qui donne : 30" 7/8

'30 7/8' parser.parse(ANS_STR)[0] ANS_PARSED.real

Pour approfondir ou réviser

http://math.cchic.ca/fractions/entier-fractionnaire