Rappel

Une fraction est le rapport entre deux nombres entiers :

$$\frac{\class{example1}{\text {nombre de parts utilisées}}}{\class{example2}{\text{nombre de parts disponibles}}}$$

Le nombre de parts utilisées est appelé numérateur, le nombre de parts disponibles est appelé dénominateur.

Exemple

On coupe un gâteau en 8 parts et on en donne 5. Il y a 5 parts utilisées sur 8 parts disponibles.

$$\frac{\class{example1}{5}}{\class{example2}{8}}$$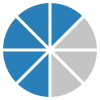

Trucs et astuces

Utilisez le dollar (1 $) pour mémoriser les fractions !!!

  • Le $\frac{1}{2}$ de 1 $ = 50 cents
  • Le $\frac{1}{4}$ de 1 $ = 25 cents
  • Le $\frac{1}{10}$ de 1 $ = 10 cents
  • Le $\frac{1}{20}$ de 1 $ = 5 cents
  • Le $\frac{1}{100}$ de 1 $ = 1 cent

1. Addition

Rappel

Pour additionner ou soustraire deux fractions avec le même dénominateur, faites l’addition ou la soustraction du numérateur et placer le résultat sur le dénominateur.

Pour additionner ou soustraire deux fractions avec un dénominateur différent, trouver le plus petit dénominateur commun voir la leçon : ppdc, convertir les fractions et faire l’addition ou la soustraction du numérateur selon la méthode ci-dessus.

Pour multiplier deux fractions, on multiplie les numérateurs et les dénominateurs. Pour diviser deux fractions, on multiplie par l’inverse de la deuxième fraction.

Exemples

$$\frac{3}{32}+\frac{11}{32}=\frac{14}{32}$$ $$\frac{1}{4}+\frac{13}{16}=\frac{4}{16}+\frac{13}{16}=\frac{17}{16}$$

Attention parce que lorsque l’on calcule il faut aller plus loin que le résultat : on ne peut donner 17 sections d’une barre de renforcement coupée en 16 ! Voir les fractions impropres.

À vous

Trouvez le résultat des additions ci-dessous, exprimez la somme en nombre mixte si besoin. Réduisez toujours la partie fractionnaire à sa plus simple expression.

Quelle est la longueur totale de la ferrure illustrée ? Exprimez le résultat en fraction ou en nombre mixte.

"

La bonne réponse est : ANS_N/ANS_D
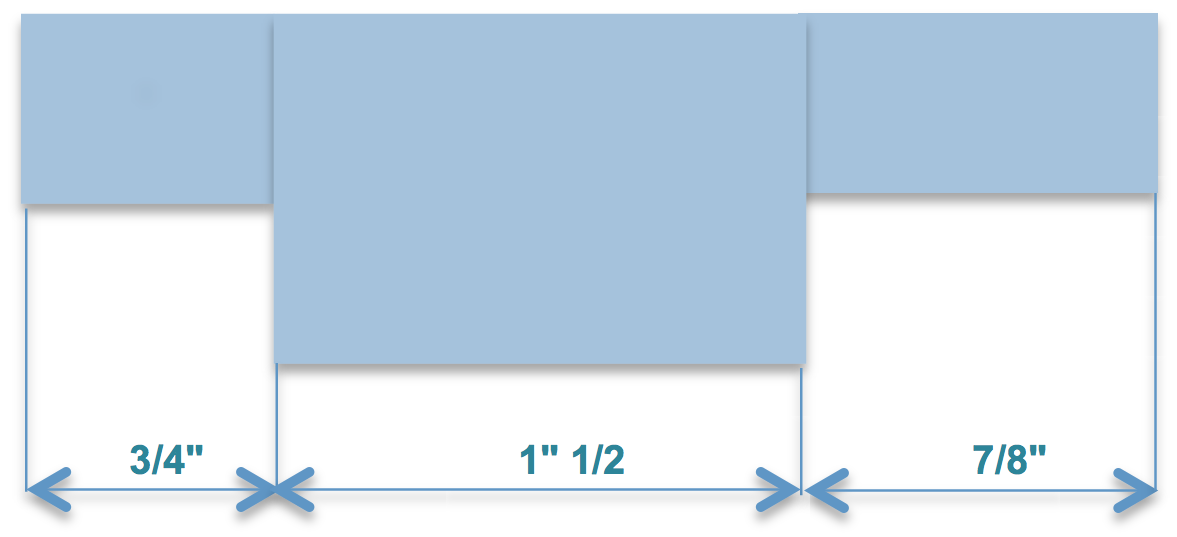
La bonne réponse est : ANS_W ANS_N/ANS_D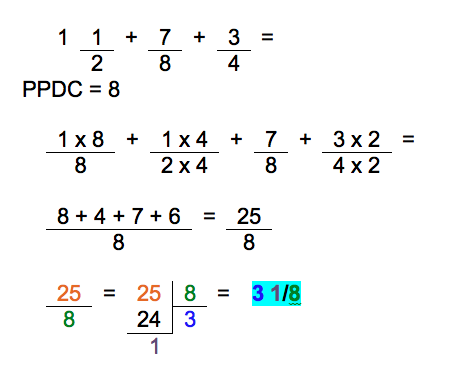
1 8 3

Une conduite d’acier mesure 15/16" de diamètre intérieur. La paroi mesure 5/32". Quel est son diamètre extérieur ? Exprimez le résultat en fraction ou en nombre mixte.

"

La bonne réponse est : ANS_N/ANS_D"
La bonne réponse est : ANS_W ANS_N/ANS_D"
$$\frac{15}{16}+\frac{5}{32}+\frac{5}{32} =$$ $$\text{PPCD} = 32$$ $$\frac{15 \times 2}{16 \times 2}+\frac{5}{32}+\frac{5}{32} =$$ $$\frac{30 + 5 + 5}{32}=\frac{40}{32}=\frac{5}{4}$$
$$\frac{\class{example1}{5}}{\class{example2}{4}} =$$
$\class{example1}{5}$$\class{example2}{4}$
$4$$\class{example3}{1}$
$1$
$$=\class{example3}{1} \frac{1}{\class{example2}{4}}$$
1 4 1

Pour approfondir ou réviser

2. Soustraction

Rappel

Pour soustraire deux fractions avec le même dénominateur, faites la soustraction du numérateur et placer le résultat sur le dénominateur.

Pour soustraire deux fractions avec un dénominateur différent, trouver le plus petit dénominateur commun (PPDC), convertir les fractions et faire la soustraction du numérateur selon la méthode ci-dessus.

Exemples

$$\frac{11}{32} - \frac{3}{32} = \frac{8}{32} = \frac{1}{4}$$ $$\frac{13}{16} - \frac{1}{4} = \frac{13}{16} - \frac{4}{16} = \frac{9}{16}$$

À vous

Trouvez le résultat des soustractions ci-dessous, exprimez la différence en nombre mixte si besoin. Réduisez toujours la partie fractionnaire à sa plus simple expression.

Le diamètre d’une meule neuve est de $13\frac{1}{8}\text{"}$, après une journée d’utilisation elle a perdu $\frac{1}{4}\text{"}$. Combien mesure-t-elle ?

"

La bonne réponse est : ANS_N/ANS_D
À la fin de la journée, la meule mesure donc : ANS_W ANS_N/ANS_D"
$$13\frac{1}{8} - \frac{1}{4} =$$ $$\text{PPDC}=8$$ $$\frac{(13 \times 8) + 1}{8} - \frac{1 \times 2}{4 \times 2} =$$ $$\frac{105}{8} - \frac{2}{8} = \frac{103}{8} =$$
$$\frac{\class{example1}{103}}{\class{example2}{8}} = $$
$\class{example1}{103}$$\class{example2}{8}$
$\phantom{1}96$$\class{example3}{12}$
$\phantom{19}7$
 $$ = \class{example3}{12} \frac{7}{\class{example2}{8}}$$
7 8 12

À vous

On enlève une section de 1/16" à une cornière mesurant 1" 31/32. Quelle est la longueur de la section restante ?

"

La bonne réponse est : ANS_N/ANS_D
Il reste donc ANS_W ANS_N/ANS_D" de la cornière.
$$1 \frac{31}{32}-\frac{1}{16} =$$ $$\text{PPDC} = 32$$ $$\frac{(1 \times 32) + 31}{32} - \frac{1 \times 2}{16 \times 2} =$$ $$\frac{63}{32} - \frac{2}{32} = \frac{61}{32} =$$
$$\frac{\class{example1}{61}}{\class{example2}{32}} = $$
$\class{example1}{61}$$\class{example2}{32}$
$32$$\class{example3}{1}$
$29$
 $$ = \class{example3}{1} \frac{29}{\class{example2}{32}}$$
29 32 1

Pour approfondir ou réviser

3. Multiplication

Rappel

Pour multiplier deux fractions, on multiplie les numérateurs et les dénominateurs.

Exemples

$$\frac{5}{8} \times \frac{2}{5} = \frac{10}{40} = \frac{1}{4}$$ $$\frac{2}{3} \times \frac{3}{10} = \frac{6}{30} = \frac{1}{5}$$

À vous

Trouvez le résultat des multiplications ci-dessous, exprimez le produit en nombre mixte si besoin. Réduisez toujours la partie fractionnaire à sa plus simple expression.

Sur un dessin d’atelier, on utilise une échelle de 1/16 pour exprimer les mesures réelles. Combien mesure la représentation d’une pièce de 118" de long ? Exprimez le résultat sous forme de nombre mixte.

"

La bonne réponse est : ANS_N/ANS_D
Sur le dessin à l’échelle 1/16, la pièce mesure ANS_W ANS_N/ANS_D" de la cornière.
$$118\times\frac{1}{16} =$$ $$\require{cancel}59 \times \cancel{2} \times \frac{1}{8 \times \cancel{2}} =$$ $$\require{cancel}\frac{59 \times \cancel{2} \times 1}{8 \times \cancel{2}} = \frac{59 \times 1}{8} = \frac{59}{8}$$
$$\frac{\class{example1}{59}}{\class{example2}{8}} = $$
$\class{example1}{59}$$\class{example2}{8}$
$56$$\class{example3}{7}$
$\phantom{5}3$
 $$ = \class{example3}{7} \frac{3}{\class{example2}{8}}$$
3 8 7

Un soudeur doit couper une tige en 20 sections de 2" 5/8. Quelle longueur doit mesurer la tige ? Exprimez le résultat sous forme de nombre mixte.

"

La bonne réponse est : ANS_N/ANS_D
La tige doit mesurer ANS_W ANS_N/ANS_D".
$$20\times2\frac{5}{8} =$$ $$\require{cancel}\cancel{2} \times \cancel{2} \times 5 \times \frac{(2 \times 8) + 5}{\cancel{2} \times \cancel{2} \times 2} =$$ $$5 \times \frac{(2 \times 8) + 5}{2} =$$ $$\frac{5 \times 21}{2} = \frac{105}{2}$$
$$\frac{\class{example1}{105}{2}} = $$
$\class{example1}{105}$$\class{example2}{2}$
$104$$\class{example3}{52}$
$\phantom{10}1$
 $$ = \class{example3}{52} \frac{1}{\class{example2}{2}}$$
1 2 52

Pour approfondir ou réviser

4. Division

Rappel

Pour diviser deux fractions, on multiplie par l’inverse de la deuxième fraction.

Exemples

$$\frac{5}{8} \div \frac{2}{5} = \frac{5}{8} \times \frac{5}{2} = \frac{25}{16}$$ $$\frac{3}{4} \div \frac{1}{4} = \frac{3}{4} \times \frac{4}{1} = \frac{12}{4} = 3$$

Remarque

Pour éviter les erreurs, il est souvent plus facile de transformer les nombres mixtes en fractions impropres (numérateur plus grand que dénominateur).

$$2\frac{5}{8} = \frac{2 \times 8}{8} + \frac{5}{8} = \frac{16 + 5}{8} = \frac{21}{8} $$

À vous

Trouvez le résultat des divisions ci-dessous, exprimez la produit en nombre mixte si besoin. Réduisez toujours la partie fractionnaire à sa plus simple expression.

Combien de sections de 1" 25/32 (perte incluse) peut-on couper dans une cornière de 45" 3/4 ? Il faut tronquer le résultat à l’entier inférieur.

pièces

On peut couper 25 pièces dans la cornière et il restera un petit morceau.
$$45 \frac{3}{4} \div 1\frac{25}{32} =$$ $$\frac{45 \times 3}{4} \div \frac{(1 \times 32) + 25}{32} =$$ $$\frac{183}{4} \div \frac{57}{32} = \frac{183}{4} \times \frac{32}{57} =$$ $$\require{cancel}\frac{\cancel{3} \times 61}{\cancel{2} \times \cancel{2}} \times \frac{\cancel{2} \times \cancel{2} \times 2 \times 2 \times 2}{\cancel{3} \times 19} =$$ $$\frac{61 x 2 x 2 x 2}{19} = \frac{488}{19}$$
$$\frac{\class{example1}{488}\class{example2}{19}} = $$
$\class{example1}{488}$$\class{example2}{19}$
$475$$\class{example3}{25}$
$\phantom{4}13$
 $$ = \class{example3}{25} \frac{13}{\class{example2}{19}}$$
25

On a une pile de tôles qui pèse 325 lb 1/2, chaque tôle pèse 11 lb 5/8. Combien y a-t-il de tôles ?

tôles

Il y a 28 tôles.
$$325 \frac{1}{2} \div 11 \frac{5}{8}$$ $$\frac{(325 \times 2) + 1}{2} \div \frac{(11 \times 8) + 5}{8}$$ $$\frac{651}{2} \div \frac{93}{8} = \frac{651}{2} \times \frac{8}{93}$$ $$\require{cancel} \frac{\cancel{31} \times 7 \times \cancel{3}}{\cancel{2}} \times \frac{\cancel{2} \times 2 \times 2}{\cancel{31} \times \cancel{3}} = \frac {7 \times 2 \times 2}{1} = 28$$
28

Pour approfondir ou réviser