Partie 1
Périmètre (1 dimension)
Exemple a
L’espace de stationnement ci-dessous mesure 175 m par 200 m. Par sécurité, on l’entoure d’une clôture. L’ouverture mesure 7,2 m. Quel est le périmètre de la clôture ?

À vous
Quel est le périmètre de la clôture ?
m2
La bonne réponse est : ANS m2
Donc :
[2 x (200 + 175)] - 7,20 = [2 x 375] – 7,20 = 742,80
Partie 2
Surface ou aire (2 dimensions)
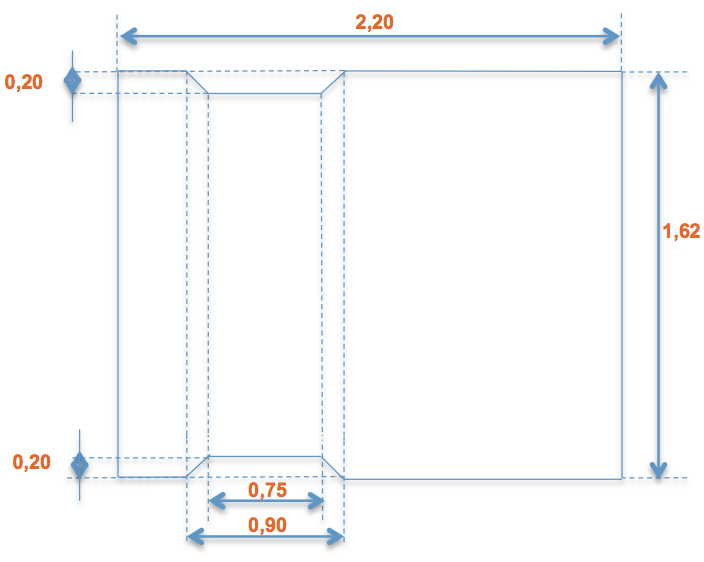
Un entrepreneur décide de protéger le sol de son fourgon à l’aide d’un plancher (voir le plan ci-dessous). La partie surélevée correspond au passage des roues arrière du fourgon.
Rappel
Pour calculer l’aire d’un trapèze (deux bases parallèles) on multiplie la somme de ses deux bases par la hauteur et on divise par le tout 2 :
[(petite base + grande base) x hauteur] ÷ 2 = Aire du trapèze.
À vous
Quelle est la surface du plancher ?
(Voir le plan ci-dessus.)
{?} m2
3.234
Donc : On calcule d’abord la surface totale. 2,20 x 1,62 = 3,564 m2
2,20 x 1,62 = 3,564 m2
Ensuite, on calcule le passage des roues (0,75 + 0,90) x 0,20 ÷ 2 = 0,165 m2
Puis on enlève deux fois le passage des roues du total. 3,564 – (0,165 x 2) = 3,234 m2
La bonne réponse est : globals.frenchFormatNumber(ANS_R) m2.