Rappel
Pour calculer le volume $V$, on multiplie les trois mesures suivants :
- Hauteur : $h$
- Largeur : $\text{L}$
- Profondeur : $p$
- Longueur : $l$
- Largeur : $\text{L}$
- Épaisseur : $é$
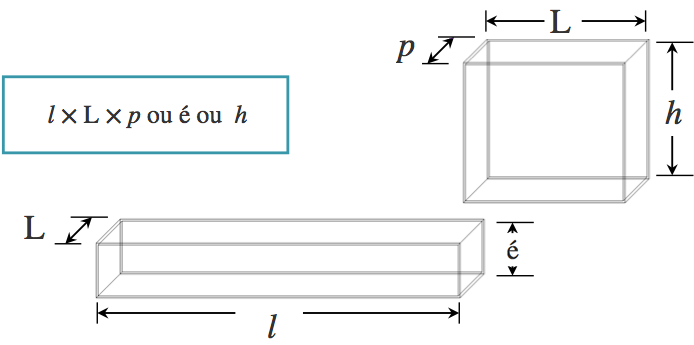
- Hauteur : $h$
- Diamètre : $d\ ou\ Ø$
- Rayon : $r$

Trucs et astuces
Le calcul des volumes adopté en industrie est effectué en arrondissant précisément à la troisième décimale près et n’arrondissez pas pendant les calculs, seulement pour le résultat !
Exemple a
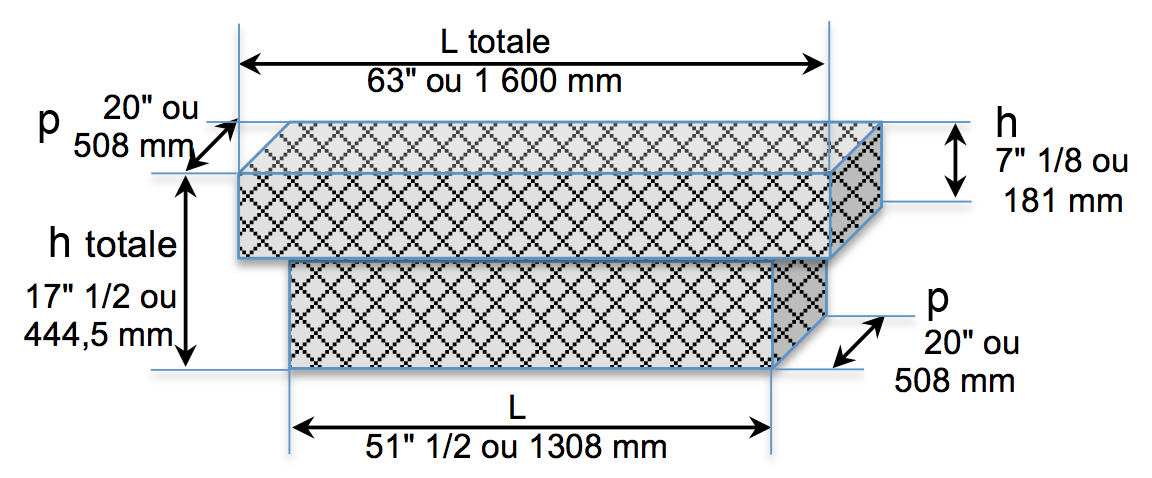
Pour calculer le volume du coffre à outils à l’arrière du fourgon en centimètres cubes, ou en pouces cubes, il faut calculer la longueur par la hauteur par la profondeur pour chaque partie et ajouter les deux.
| Partie haute | |
|---|---|
| Longueur totale | 63" ou 1 600 mm |
| Hauteur | 7" 1/8 ou 181 mm |
| Profondeur | 20" ou 508 mm |
| Partie basse | |
|---|---|
| Longueur | 51" 1/2 ou 1308 mm |
| Hauteur totale - hauteur partie haute | 17 1/2" - 7 1/8" = 10 1/8" ou 444,5 mm - 181 mm = 263,5 mm |
| Profondeur | 20" ou 508 mm |
Exemple b
La conversion des pouces en millimètres ne donne pas des mesures précises (dixièmes de millimètres). Pour de gros volumes (mètre cube), l’imprécision devient problématique (voir le module Utilisation du système impérial et du système métrique).
Pour ne pas avoir de chiffres trop longs à calculer, convertissez vos mesures en centimètres.
Partie haute : 1 600 mm x 181 mm x 508 mm = 160 cm x 18,1 cm x 50,8 cm = 147 116,8 cm3
Partie basse : 1 308 mm x 263,5 mm x 508 mm = 130,8 cm x 26,35 cm x 50,8 cm = 175 086,264 cm3
Total : 147 116,8 + 175 086,264 = 322 203,084 cm3
En pouce, cela donne :
Partie haute : 63" x 7" 1/8 x 20" = 63" x 7,125" x 20" = 8 977,5 po3
Partie basse : 51" 1/2 x 10" 1/8 x 20" = 51,5" x 10,125" x 20" = 10 428,75 po3
Total : 8 977,5 + 10 428,75 = 19 406,25 po3
1 po3 ≈ 16,387 064 cm3, soit 19 406,25 x 16,387 064 ≈ 318 011,460 75 cm3 ou 318 011,461 cm3 arrondi au millième.
Le résultat obtenu n’est donc pas tout à fait identique. Il y a plus de 4 000 cm3 d’écart ou plus de 255 po3 (4 191,623 cm3 soit 255,789 po3). Pour cette raison, vous utiliserez de préférence les mesures métriques pour calculer les volumes.
Exemple c
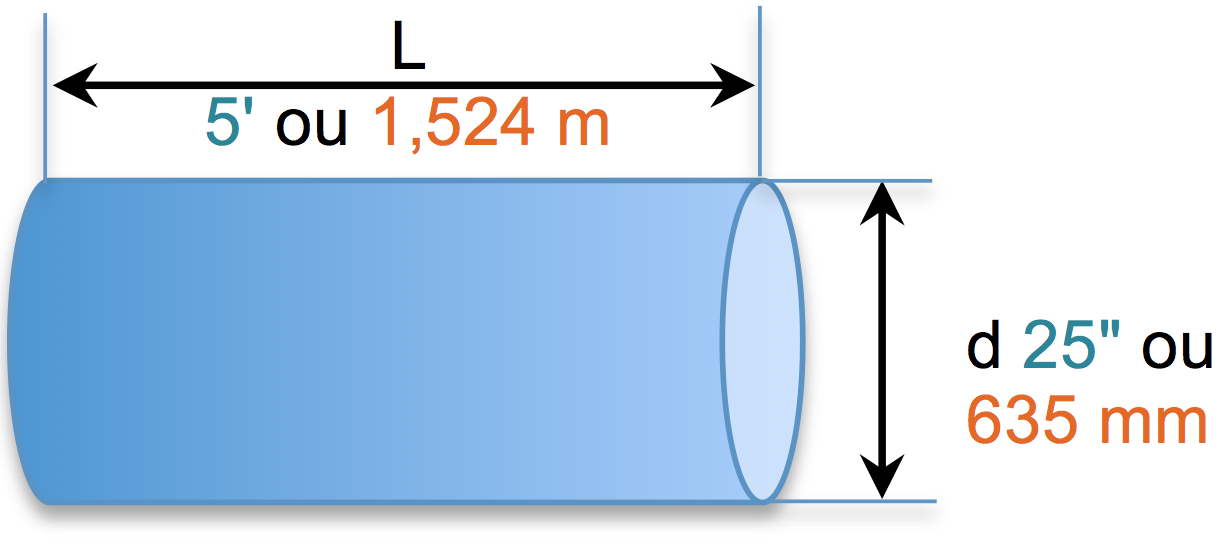
Une conduite a un diamètre de 635 mm (25") et une longueur de 1,524 m (5') de long. Quel volume en litres peut contenir cette conduite ?
À vous
Quel volume en litres peut contenir cette conduite ?
{?} litres
La bonne réponse est ANS.
(635 mm ÷ 2)2 x 1,524 m x π = ???
Trucs et astuces :
convertissez toutes les mesures dans la même unité.
635 mm = 0,635 m
(0,635m÷2)2 x 1,524m x π ≈
0,100 806 25 x 1,524 x π ≈
0,153 628 725& x π ≈
0,482 638 873 84 m3
Remarque :
1 m3 = 1000 l
Donc :
482,638 873 84 l ou 482,639 l arrondi au millième
Remarque
Utiliser les mesures métriques pour calculer les volumes
Pourquoi ?
Une conduite a un diamètre de 635 mm (25") et une longueur de 1,524 m (5') de long. Quel volume en gallons peut contenir cette conduite ?
En pied, cela donne :
(25"÷2)2 x 5' x π= ???
25" = 25/12' = 2,083 333...'
(2,083 333...'÷2)2 x 5' x π ≈
1,041 666...2 x 5' x π ≈
1,085 069 444 x 5' x π ≈
5,425 347 222 x π ≈
17,044 230 976 pi3
Remarque :
1 pi3 = 6,228 835 5 gal
Donc :
106,165 710 977 gal ou 106,166 gal arrondi au millième
Remarque :
1 gal = 4,546 09 l
14,676 gal ≈ 482,640 190 94 l ou 482,640 l arrondi au millième
Le résultat obtenu n’est donc pas tout à fait identique. Il a plus de 1⁄2 l ou 2 tasses 1⁄4 d’écart.
Pour cette raison, vous utiliserez de préférence les mesures métriques pour calculer les volumes.