À vous
Mesures linéaires
2 points par bonne réponse
Des fentes doivent être découpées dans une plaque selon le schéma ci-contre. Quelle est la longueur de la rainure B ? Donnez vos résultats en millimètres et en pouces.
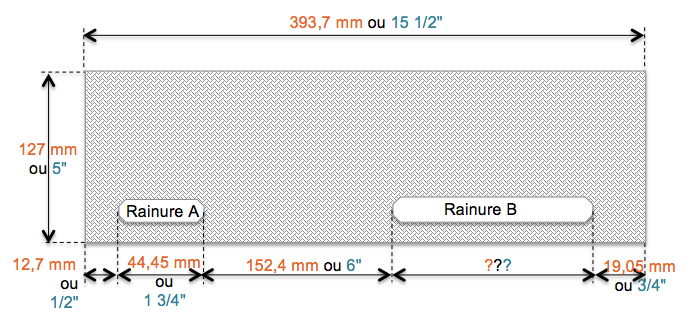
Longueur de la rainure B (mm) : mm
Donc, longueur totale - (longueur à gauche de la fente A + longueur de la fente A + longueur entre les deux fentes + longueur à droite de la fente B) = longueur de la fente B
393,7 - (12,7 - 44,45 - 152,4 - 19,05) = 165,1 mm
La bonne réponse est : 165,1 mm.
Longueur de le rainure B (po.) : {?} po.
On convertit en décimale de pouce ou on fait une addition de fraction :
- 15 1/2" = 15,5"
- 1/2" = 0,5"
- 1 3/4" = 1,75"
- 3/4" = 0,75"
- 15,5 - (0,5 + 1,75 + 6 + 075) = 6,5"
- 6 1/2"
6 1/2"
Mesures d’aires
2 points par bonne réponse
Donnez vos réponses à 3 décimales près.
Une plaque d’acier circulaire est coupée à la flamme et le centre est retiré. Quelle est la surface totale de la plaque et de la partie enlevée ? Donnez vos mesures en cm2 et en po2.
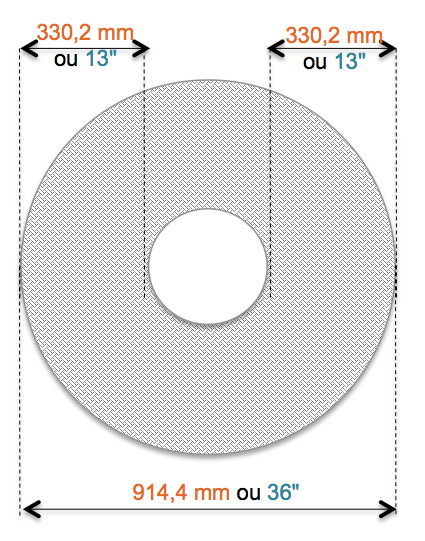
Quelle est la surface totale (cm2) ?
{?} cm2
La bonne réponse est : 6 566,929 cm2.
On calcule la surface totale, soit r2 x π ≈ r = 914,4 mm ÷ 2 = 45,72 cm donc 45,722 x π ≈ 6 566,928 929 1 cm2 soit 6 566,929 cm2 arrondi au millième
Remarque, si on veut calculer l’aire de la partie restante, on prend les chiffres non arrondis pour obtenir le résultat le plus précis possible.
Quelle est la surface de la partie enlevée (cm2) ?
{?} cm2
La bonne réponse est : 506,707 cm2.
On calcule la partie enlevée :
r = [914,4 - (330,2 x 2)] ÷ 2 = 12,7 cm
donc 12,72 x π ≈ 506,707 479 097 cm2
soit 506,707 cm2 arrondi au millième
Quelle est la surface totale (po2) ?
{?} po2
La bonne réponse est : 1 017,876 po2.
On calcule la surface totale :
r = 36" ÷ 2 = 18"
donc 182 x π ≈ 1 017,876 019 76 po2
soit 1 017,876 po2 arrondi au millième
Quelle est la surface de la partie enlevée (po2) ?
{?} po2
La bonne réponse est : 78,540 po2.
On calcule la partie enlevée :
r = [36 - (13 x 2)] ÷ 2 = 5"
donc 52 x π ≈ 78,539 816 339 po2
soit 78,540 po2 arrondi au millième
Mesures de volumes
2 points par bonne réponse
L’acier est vendu au poids. Pour les plaques, l’entrepreneur va acheter ses pièces selon la taille en mètres carrés ou en pieds carrés et le prix sera indiqué en fonction des kilogrammes par mètre carré (kg/m2), ou des livres par pied carré (lb/pi2). Pour les poutres, les profilés d’angle ou les barres c’est le volume qui va déterminer le prix. Quel est le volume de la barre à section rectangulaire laminée à froid et du profilé rond ci-contre. Donnez vos résultats en pouce cube (po3) et en centimètre cube (cm3).
Dimensions barre rectangulaire :
Longueur : 22" ou 558 mm
largeur : 2" ou 50,8 mm
épaisseur : 1" ou 25,4 mm
Dimensions profilé rond :
hauteur : 20" ou 508 mm
diamètre : 1" ou 25,4 mm
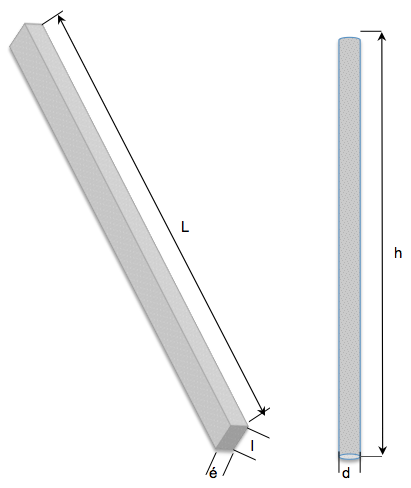
Barre rectangulaire, volume en po3 : (Donnez vos réponses à 3 décimales près.)
po3
La bonne réponse est : 44 po3.
Profilé rond, volume en po3 : (Donnez vos réponses à 3 décimales près.)
po3
La bonne réponse est : 17,279 po3.
r = 1 ÷ 2 = 0,5 ou 1/2"
Donc 22 x 0,52 x π ≈ 17,278 759 po3
soit 17,279 po3 arrondi au millième
Volume barre, volume en cm3 : (Donnez vos réponses à 3 décimales près.)
cm3
La bonne réponse est : 719,999 cm3.
Donc 558 x 50,8 x 25,4 = 719 998,6 m3
soit 719,999 cm3 arrondi au millième
Profilé rond, volume en cm3 : (Donnez vos réponses à 3 décimales près.)
cm3
La bonne réponse est : 257,407 cm3.
Volume profilé :
r = 25,4 ÷ 2 = 12,7 mm
Donc 508 x 12,72 x π ≈ 257 407,399 382 mm3
soit 257,407 cm3